Question

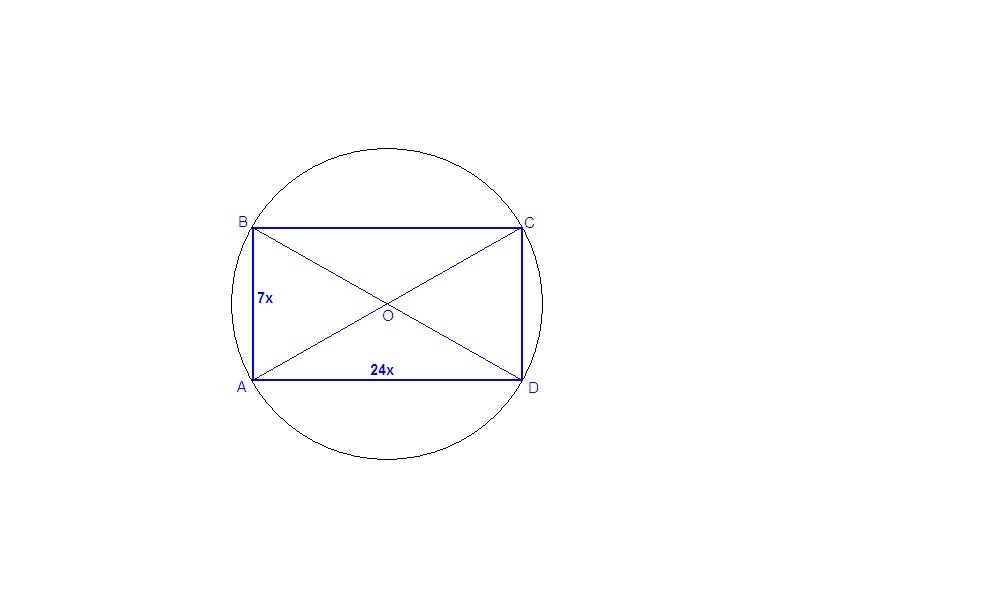
Вершины прямоугольника принадлежат окружности с радиусом 50 мм. Найдите стороны прямоугольника, учитывая, что они относятся как 7 : 24.

Answer 1

Центр окружности, описанной около прямоугольника, лежит в точке пересечения его диагоналей. Тогда диагональ прямоугольника равна диаметру окружности (диагонали прямоугольника равны).

АС = ВD = 2 · 50 = 100 мм

Пусть х - одна часть, тогда

АВ = 7х

AD = 24x.

Из прямоугольного треугольника ABD по теореме Пифагора составим уравнение:

AB² + AD² = BD²

(7x)² + (24x)² = BD²

49x² + 576x² = 10000

625x² = 10000

x² = 16

x = 4 или x = - 4 (не подходит по смыслу задачи)

АВ = 7 · 4 = 28 мм

AD = 24 · 4 = 96 мм