Предмет: Алгебра,
автор: TRESAD12
Решите уравнения:
1) (x² - 5x)(x² - 5x + 10) + 24 = 0
2)
( первое необязательно )
Приложения:
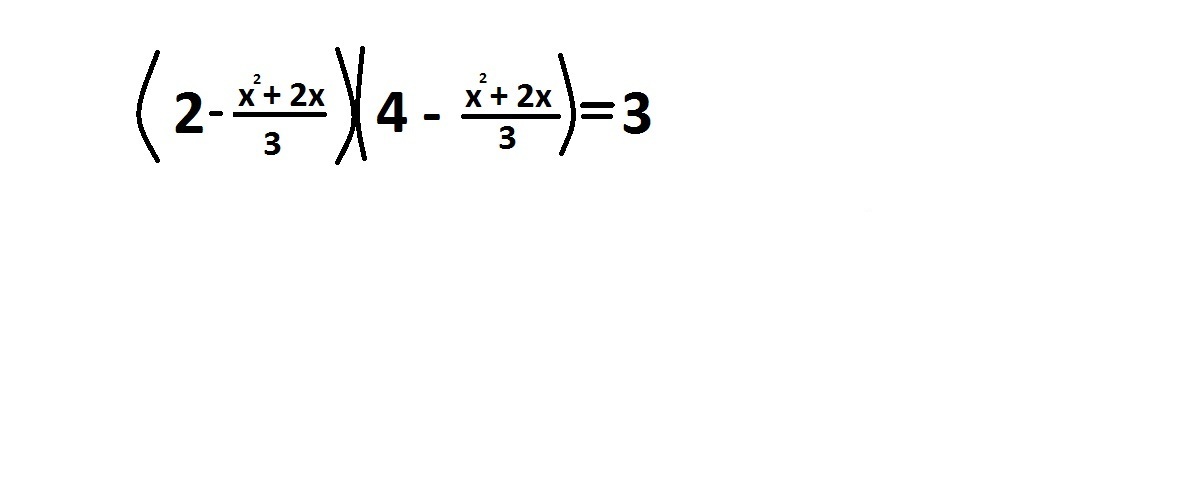
Ответы
Автор ответа:
1
1)
(х² - 5х )(х² - 5х + 10) + 24 = 0
замена х² - 5х = t
t(t + 10) + 24 = 0
t² + 10t + 24 = 0
D = 10² - 4*1*24 = 100 - 96 = 4 = 2²
D> 0 - два корня уравнения
t₁ = (-10 - 2)/(2*1) = -12/2 = -6
t₂ = (-10 + 2)/(2*1) = -8/2 = - 4
x² - 5x = - 6
x² - 5x + 6 = 0
D = (-5)² - 4*1*6 = 25 - 24 = 1 = 1²
D>0 - два корня уравнения
x₁ = (- (-5) - 1)/ (2*1) = (5 - 1)/2 = 4/2 = 2
x₂ = (- (-5) +1)/(2*1) = (5+1)/2 = 6/2 = 3
x² - 5x = - 4
x² - 5x + 4 = 0
D = (-5)² - 4*1*4 = 25 - 16 = 9 = 3²
D>0 - два корня уравнения
x₁ = (- (-5) - 3)/(2*1) = (5-3)/2 = 2/2 = 1
x₂ = (- (-5) + 3)/(2*1) = (5+3)/2 = 8/2 = 4
Ответ: х₁ = 1 ; х₂ = 2 ; х₃ = 3 ; х₄ = 4 .
2)
(2 - (х² +2х)/3 ) ( 4 - (х² + 2х)/3 ) = 3
замена: (х² + 2х)/3 = t
(2 - t)(4 - t) = 3
8 - 2t - 4t + t² - 3 = 0
t² - 6t + 5 = 0
D= (-6)² - 4*1*(-5) = 36 - 20 = 16 = 4²
D>0 - два корня уравнения
t₁ = (- (-6) - 4)/(2*1) = (6 - 4)/2 = 2/2 = 1
t₂ = (- (-6) + 4)/(2*1) = (6 + 4)/2 = 10/2 = 5
(x² + 2x)/3 = 1
x² + 2x = 1*3
x² +2x - 3 = 0
D = 2² - 4*1*(-3) = 4+12 = 16 = 4²
D>0 - два корня уравнения
x₁ = (-2 - 4)/(2*1) = -6/2 = - 3
x₂ = (-2 +4)/(2*1) = 2/2 = 1
(х² + 2х)/3 = 5
х² + 2х = 5 * 3
х² + 2х - 15 = 0
D = 2² - 4*1*(-15) = 4 + 60 = 64 = 8²
D>0 - два корня уравнения
х₁ = (-2 - 8)/(2*1) = -10/2 = - 5
х₂ = (-2 +8)/(2*1) = 6/2 = 3
Ответ : х₁ = - 5 ; х₂ = - 3 ; х₄ = 1 ; х₅ = 3.
(х² - 5х )(х² - 5х + 10) + 24 = 0
замена х² - 5х = t
t(t + 10) + 24 = 0
t² + 10t + 24 = 0
D = 10² - 4*1*24 = 100 - 96 = 4 = 2²
D> 0 - два корня уравнения
t₁ = (-10 - 2)/(2*1) = -12/2 = -6
t₂ = (-10 + 2)/(2*1) = -8/2 = - 4
x² - 5x = - 6
x² - 5x + 6 = 0
D = (-5)² - 4*1*6 = 25 - 24 = 1 = 1²
D>0 - два корня уравнения
x₁ = (- (-5) - 1)/ (2*1) = (5 - 1)/2 = 4/2 = 2
x₂ = (- (-5) +1)/(2*1) = (5+1)/2 = 6/2 = 3
x² - 5x = - 4
x² - 5x + 4 = 0
D = (-5)² - 4*1*4 = 25 - 16 = 9 = 3²
D>0 - два корня уравнения
x₁ = (- (-5) - 3)/(2*1) = (5-3)/2 = 2/2 = 1
x₂ = (- (-5) + 3)/(2*1) = (5+3)/2 = 8/2 = 4
Ответ: х₁ = 1 ; х₂ = 2 ; х₃ = 3 ; х₄ = 4 .
2)
(2 - (х² +2х)/3 ) ( 4 - (х² + 2х)/3 ) = 3
замена: (х² + 2х)/3 = t
(2 - t)(4 - t) = 3
8 - 2t - 4t + t² - 3 = 0
t² - 6t + 5 = 0
D= (-6)² - 4*1*(-5) = 36 - 20 = 16 = 4²
D>0 - два корня уравнения
t₁ = (- (-6) - 4)/(2*1) = (6 - 4)/2 = 2/2 = 1
t₂ = (- (-6) + 4)/(2*1) = (6 + 4)/2 = 10/2 = 5
(x² + 2x)/3 = 1
x² + 2x = 1*3
x² +2x - 3 = 0
D = 2² - 4*1*(-3) = 4+12 = 16 = 4²
D>0 - два корня уравнения
x₁ = (-2 - 4)/(2*1) = -6/2 = - 3
x₂ = (-2 +4)/(2*1) = 2/2 = 1
(х² + 2х)/3 = 5
х² + 2х = 5 * 3
х² + 2х - 15 = 0
D = 2² - 4*1*(-15) = 4 + 60 = 64 = 8²
D>0 - два корня уравнения
х₁ = (-2 - 8)/(2*1) = -10/2 = - 5
х₂ = (-2 +8)/(2*1) = 6/2 = 3
Ответ : х₁ = - 5 ; х₂ = - 3 ; х₄ = 1 ; х₅ = 3.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: m45026232
Предмет: Английский язык,
автор: angelinalusnikova286
Предмет: Математика,
автор: palashkinasasha
Предмет: Математика,
автор: Утя11