Question

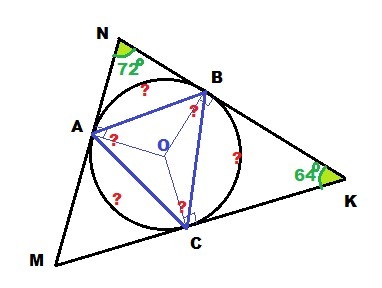
Окружность с центром О касается сторон MN,NK,MK треугольника MNK в точках А,В и С соответственно.Найдите дуги АВ,ВС,АС и углы треугольника ABC , если угол MNK=72, угол NKM=64

Answer 1

Нужно использовать следующие свойства:
Окружность вписана в треугольник, стороны треугольника - касательные к окружности. 
Радиус в точку касания образует угол 90° с касательной.
Сумма углов любого четырёхугольника равна 360°.
Центральный угол равен дуге, на которую опирается.
Вписанный угол равен половине дуги, на которую опирается.

ΔMNK:   ∠N = 72°; ∠K = 64°  ⇒ 
 ∠M = 180°-∠N - ∠K = 180° - 72° - 64° = 44°

Четырёхугольник OBKC
∠BOC = 360° - ∠OBK - ∠OCK - ∠K = 
           = 360° - 90° - 90° - 64° = 116°
Дуга ∪BC = ∠BOC = 116°
∠BAC = ∪BC/2 = 116°/2 = 58°

Четырёхугольник OANB
∠AOB = 360° - ∠OBN - ∠OAN - ∠N = 
           = 360° - 90° - 90° - 72° = 108°
Дуга ∪AB = ∠AOB = 108°
∠ACB = ∪AB/2 = 108°/2 = 54°

Четырёхугольник OCMA
∠AOC = 360° - ∠OAM - ∠OCM - ∠M = 
           = 360° - 90° - 90° - 44° = 136°
Дуга ∪AC = ∠AOC = 136°
∠ABC = ∪AC/2 = 136°/2 = 68°

Ответ:  дуги:  ∪AB =108°;  ∪AC =136°;  ∪BC =116°
           Углы ΔABC:   ∠A = 58°;  ∠B = 68°;  ∠C = 54°