Предмет: Математика,
автор: НиколайСПБ
Помогите найти значения. Задание отображено на рисунке.
Приложения:
sedinalana:
можно задание словами?
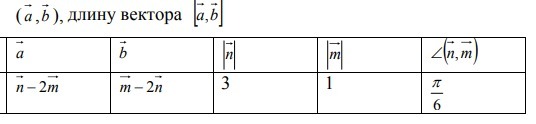
Найти а->,b->; найти длину вектора [a->,b->]
(а->,b->)
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: История,
автор: gubina1905
Предмет: Химия,
автор: tihonigry
Предмет: География,
автор: glebahleb125
Предмет: Математика,
автор: лоидв