Question

В равнобедренной трапеции ABCD с основаниями AD=25 и BC=7 боковая сторона равна 15. Найдите радиус окружности, описанной около треугольника ABD.

Answer 1

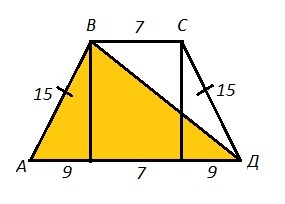
АВСД - трапеция , АД=25,  ВС=7  ,  АВ=СД=15
Опустим ⊥ из точки В и из точки С на АД. Обозначим их ВН и СМ.
АН=ДМ=(АД-ВС)/2=(25-7)/2=9 , НМ=ВС=7 
ΔАВН:  ВН=√(АВ²-АН²)=√(15²-9²)=12
ΔВДН:  ВД=√(ВН²+ДН²)=√(16²+12²)=20
Радиус описанной окр. около ΔАВД ищем из формулы:
R=abc/4S
S=1/2*AД*ВН=1/2*12*25=150
R=(15*20*25)/(4*150)=12,5  -  радиус описанной окр. около ΔАВД.