Предмет: Математика,
автор: Аноним
Решите плизз) ❤️даю 100 баллов. Найдите общее решение дифференциального уравнения. y^2+x^2*y’=xy*y’
Приклепила изображение
Приложения:
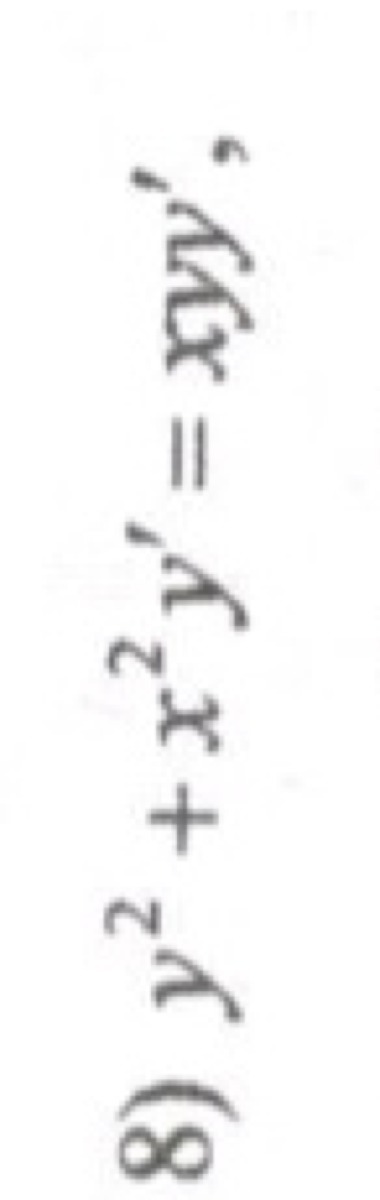
Ответы
Автор ответа:
0
Разделим обе части уравнения на x². Мы получим уравнение (y/x)²+y'=(y/x)*y'. Положим теперь y/x=z, тогда y=z*x и y'=z+x*z'. Подставляя эти выражения в уравнения, получим уравнение z²+z+x*z'=z*(z+x*z'), или z+x*z'=x*z*z'. Отсюда x*z'*(z-1)=z, z'*(z-1)=z/x, z'*(z-1)/z=1/x. Но так как z'=dz/dx, то, умножая обе части на dx, приходим к уравнению (z-1)*dz/z=dx/x, или dz-dz/z=dx/x. Интегрируя обе части, получаем z-ln(z)=ln(x)+ln(C), или z-ln(z)=ln(x*C), где C>0 - произвольная постоянная. Заменяя теперь z на y/x, получаем y/x-ln(y/x)=ln(x*C), y/x-ln(y)+ln(x)=ln(x*C), y/x-ln(y)=ln(C). Полагая теперь ln(C)=C1, окончательно получаем y/x-ln(y)=C1.
Проверка: продифференцируем полученное равенство по x: (y'*x-y)/x²-y'/y=0. Умножив теперь обе части на произведение x²*y, получим x*y*y'-y²-x²*y'=0, или y²+x²*y'=x*y*y', то есть мы пришли к исходному уравнению. Значит, решение найдено верно.
Ответ: y/x-ln(y)=C1.
Проверка: продифференцируем полученное равенство по x: (y'*x-y)/x²-y'/y=0. Умножив теперь обе части на произведение x²*y, получим x*y*y'-y²-x²*y'=0, или y²+x²*y'=x*y*y', то есть мы пришли к исходному уравнению. Значит, решение найдено верно.
Ответ: y/x-ln(y)=C1.
Vasily1975:
Замечание: в данном случае полученное равенство, называемое общим интегралом уравнения, неразрешимо относительно y, то есть из него нельзя выразить y как функцию от x. Но этого и не требуется, так как общий интеграл тоже является решением уравнения.
Похожие вопросы
Предмет: Математика,
автор: wikaiw2010
Предмет: Математика,
автор: Abulkhair2
Предмет: История,
автор: chupruvvasya
Предмет: Математика,
автор: Лёлькин1
Предмет: Физика,
автор: даданет