Предмет: Алгебра,
автор: markonseon2001
Срочно помощь по Алгебре! 20 баллов!
Докажите тождество (на картинке).
Приложения:
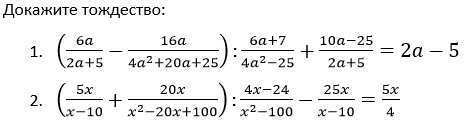
Ответы
Автор ответа:
0
Левую часть тождества приравняли к правой, значит тождество верно.
Левую часть тождества приравняли к правой, значит тождество верно.
markonseon2001:
Эм... а второе решение?
Готово.
Спасибо.
Похожие вопросы
Предмет: Математика,
автор: sar780037
Предмет: Геометрия,
автор: Kamosyakamosya
Предмет: Математика,
автор: masakosmal923
Предмет: Математика,
автор: Tatyana1955
Предмет: Литература,
автор: Winx20022