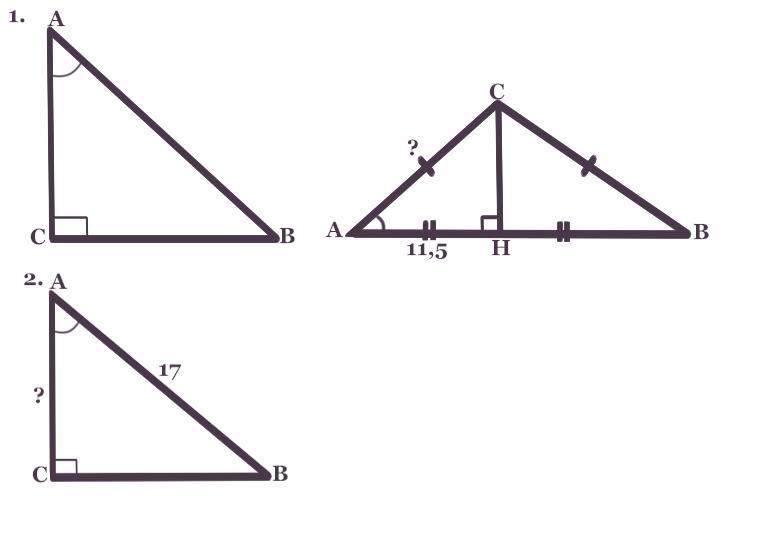
В треугольнике АВС угол С равен 90 градусов. Найдите TgA
В треугольнике АВС угол С равен 90 градусов , АВ=17. Найдите АС
В треугольнике АВС АС=ВС, АВ=23. Найдите АС
Ответы
1)
Дано :
ΔАВС - прямоугольный (∠С = 90°).
Найти :
Tg(∠A) = ?
Решение :
- Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему катету.
Для ∠А :
Катет СВ - противолежащий
Катет АС - прилежащий.
Тогда по выше сказанному -
Ответ :
- - -
2)
Дано :
ΔАВС - прямоугольный (∠С = 90°).
АВ = 17.
Найти :
АС = ?
Решение :
(по определению косинуса острого угла прямоугольного треугольника).
ИЛИ :
(Так как sin(∠B) = cos(∠A), то есть это одни и те же функции).
Ответ :
17*cos(∠A) или 17*sin(∠B).
- - -
3)
Дано :
ΔАВС.
АС = ВС.
АВ= 23.
Найти :
АС = ?
Решение :
Так как АС = ВС (по условию), то ΔАВС - равнобедренный (по определению).
Проведём из вершины С на основание АВ высоту СН, которая по свойству высоты в равнобедренном треугольнике, проведённой к основанию, является медианой.
Тогда по определению медианы -
АН = НВ = 0,5*АВ = 0,5*23 = 11,5.
Рассмотрим ΔАНС - прямоугольный.
(по определению косинуса острого угла прямоугольного треугольника).
ИЛИ :
(так как sin(∠АСН) и cos(∠A) - одни и те же функции).
Ответ :
или
.