Предмет: Алгебра,
автор: tatiana310
Решите уравнение: 18/x^2-9 = x/x+3 + 4/x-3.
Ответы
Автор ответа:
23
.................................
Приложения:
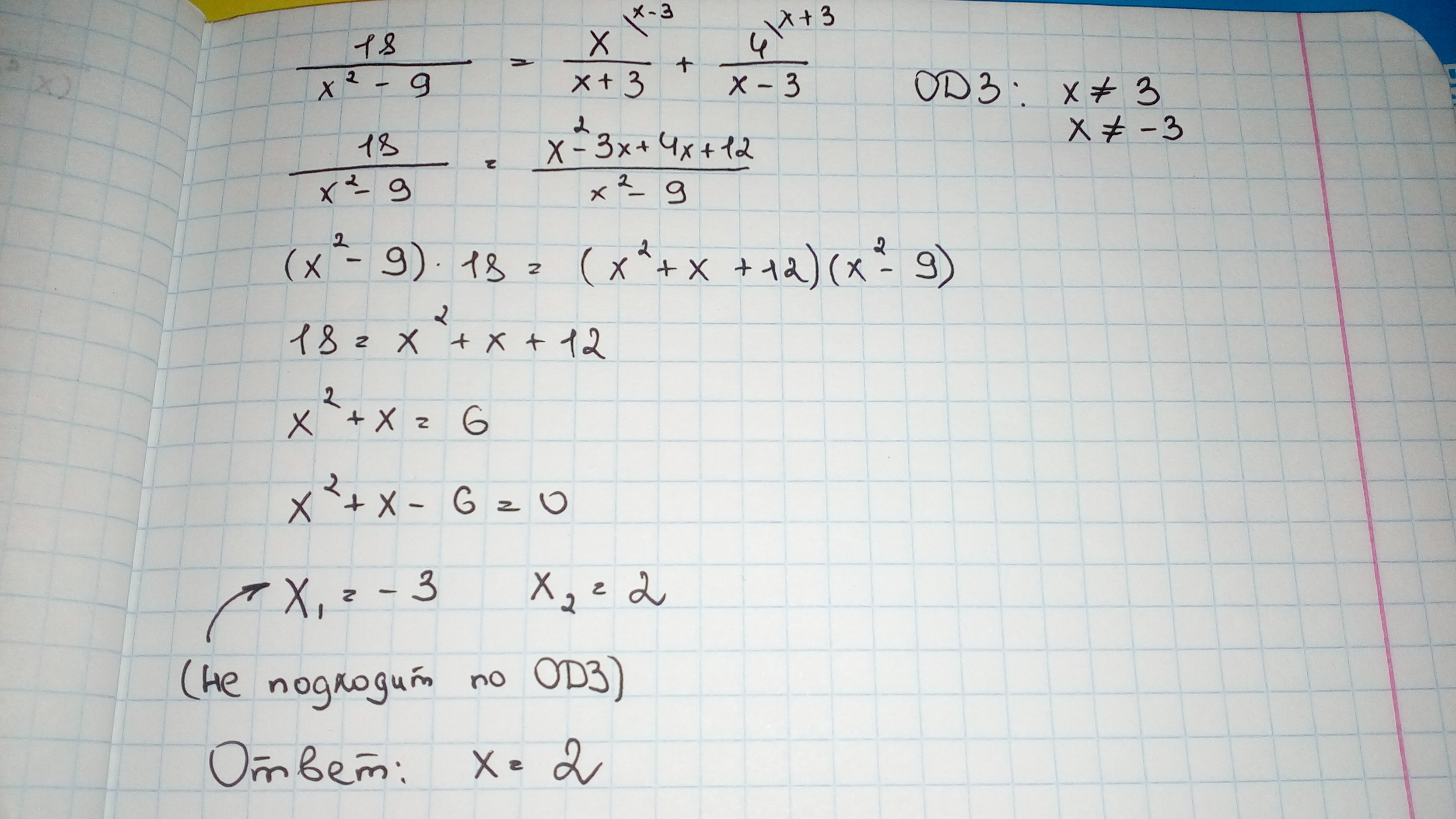
tatiana310:
спасибо
Автор ответа:
7
18/(х+3)(х-3)-х/х+3-4/х-3=0
18-х^2+3x-4x-12/(x+3)(x-3)=0
-x^2-x+6/(x+3)(x-3)=0
x^2+x-6/(x+3)(x-3)=0
(x+3)(x-2)/(x+3)(x-3)=0
x не равен 3, х не равен -3
х-2=0
х=2
Здесь использована формула разность квадратов. Привели к общему знаменателю. Решили квадратичное уравнение по теореме Виета. Сделали анализ, что делить на нуль нельзя и исключили лишние корни.
18-х^2+3x-4x-12/(x+3)(x-3)=0
-x^2-x+6/(x+3)(x-3)=0
x^2+x-6/(x+3)(x-3)=0
(x+3)(x-2)/(x+3)(x-3)=0
x не равен 3, х не равен -3
х-2=0
х=2
Здесь использована формула разность квадратов. Привели к общему знаменателю. Решили квадратичное уравнение по теореме Виета. Сделали анализ, что делить на нуль нельзя и исключили лишние корни.
спасибо)
Похожие вопросы
Предмет: География,
автор: ludmilapalij9
Предмет: Биология,
автор: timyr150808
Предмет: Қазақ тiлi,
автор: UzumakiNarutoKurama
Предмет: Математика,
автор: НикУаилд
Предмет: Математика,
автор: Нижнекамс