Question

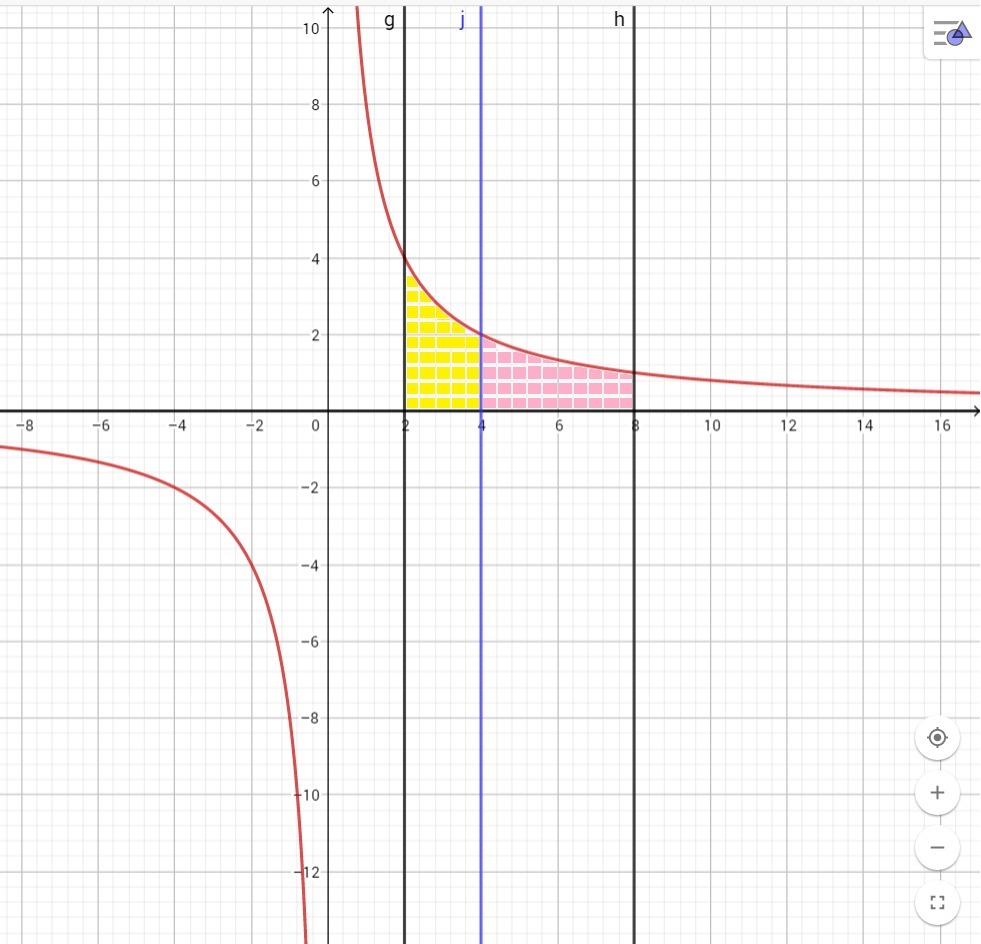
Будь ласка, допоможіть дуже Вас прошу!При якому значенні а пряма x=a ділить площу фігури, обмеженої графіком функції f(x)=8/x і прямими y=0,x=2,x=8, навпіл ?

Answer 1

Площадь фигуры (площадь криволинейной трапеции) численно равна определенному интегралу.

По условию 2 < a < 8.

Площадь левой половины:

$S = \int\limits^a_2 {\frac{8}{x}} \, dx = 8ln|x||_{2}^{a} = (8lna) - (8ln2) = 8(lna - ln2) = 8ln \frac{a}{2}$

Площадь правой половины:

$S = \int\limits^8_a {\frac{8}{x}} \, dx = 8ln|x||_{a}^{8} = (8ln8) - (8lna) = 8(ln8 - lna) = 8ln \frac{8}{a}$

По условию площади должны быть равны, имеем логарифмическое равенство:

$8ln \frac{a}{2} = 8ln \frac{8}{a}$
$ln \frac{a}{2} = ln \frac{8}{a}$
$\frac{a}{2} = \frac{8}{a}$
a² = 16
a = 4

Ответ: а = 4.