Предмет: Геометрия,
автор: Радочка2016
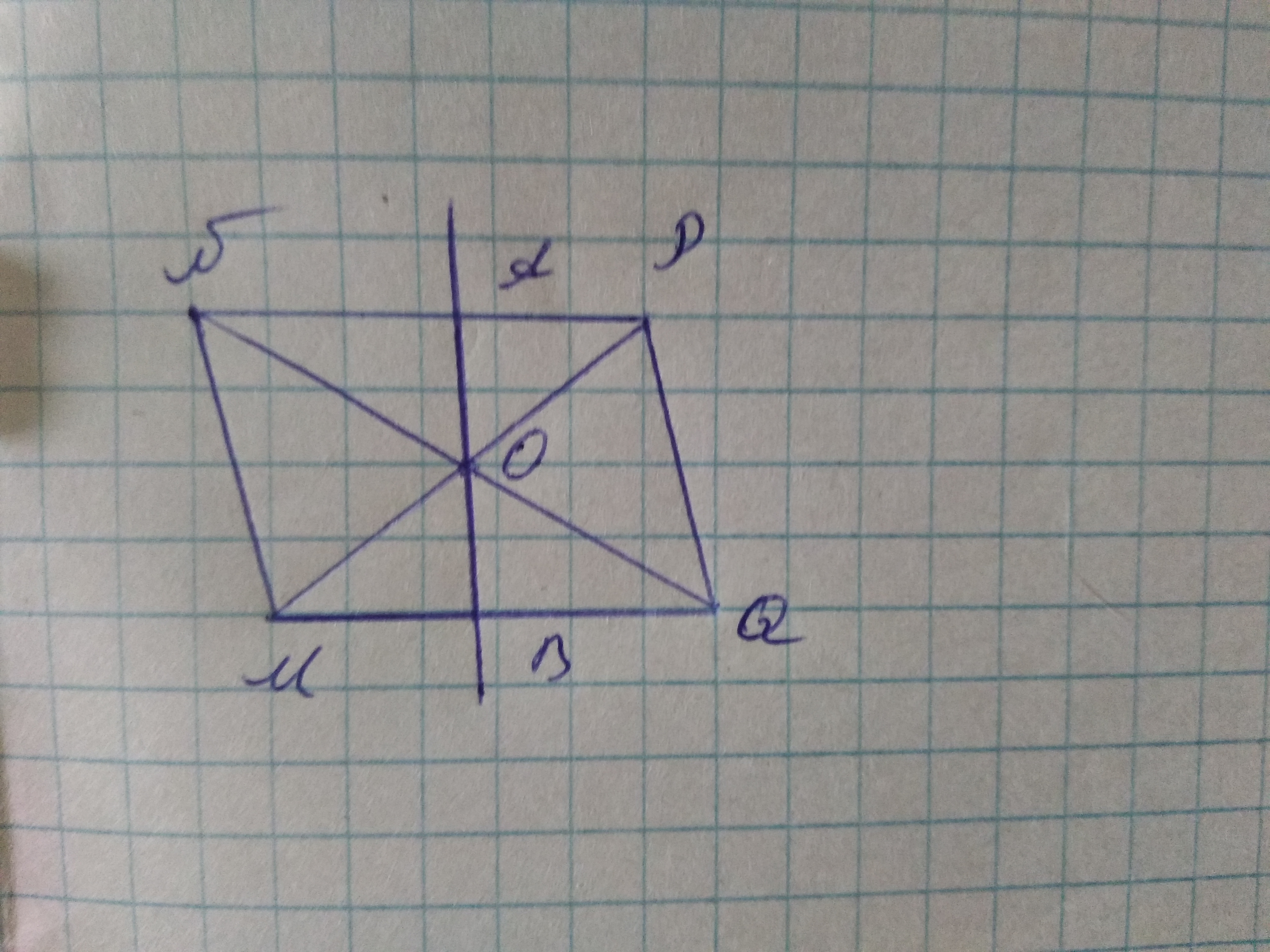
В параллелограмме MNPQ через точку О пересечения диагоналей проходит прямая , пересекающая NP и MQ в точках А и В. а) Докажите, что АО=ОВ б) Найдите NP , NA =3 см, MB =2см
Ответы
Автор ответа:
3
а) Рассмотрим ΔMBO и ΔAPO
1) ∠AOP=∠MOB - как вертикальные углы
2) ∠OMB=∠APO - как накрест лежащие углы при параллельных прямых NP и MQ и секущей MP. (NP//MQ - по определению параллелограмма)
3) MO=OP - по свойству параллелограмма (точкой пересечения делит диагонали пополам)
Значит ΔMBO и ΔAPO равны по двум углам и стороной между ними. Следовательно AO=OB - как соответственно равные элементы в равных треугольниках.
б) 1) Из пункта а) ΔMBO = ΔAPO, значит MB=AP=2 см - как соответственно равные элементы в равных треугольниках.
2) NP=NA+AP=3+2=5см
1) ∠AOP=∠MOB - как вертикальные углы
2) ∠OMB=∠APO - как накрест лежащие углы при параллельных прямых NP и MQ и секущей MP. (NP//MQ - по определению параллелограмма)
3) MO=OP - по свойству параллелограмма (точкой пересечения делит диагонали пополам)
Значит ΔMBO и ΔAPO равны по двум углам и стороной между ними. Следовательно AO=OB - как соответственно равные элементы в равных треугольниках.
б) 1) Из пункта а) ΔMBO = ΔAPO, значит MB=AP=2 см - как соответственно равные элементы в равных треугольниках.
2) NP=NA+AP=3+2=5см
Приложения:
Похожие вопросы
Предмет: Физика,
автор: podliva2345
Предмет: Алгебра,
автор: magamagov039
Предмет: Русский язык,
автор: lrrrrrxs
Предмет: Математика,
автор: lynegof
Предмет: Алгебра,
автор: Myso777