Предмет: Алгебра,
автор: vasilisaminaeva1
найдите сумму наименьшего и наибольшего значений функции y=4x^2+1/x на отрезке [1/4;1]
Приложения:
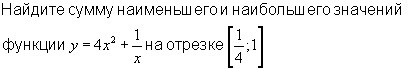
mionkaf1:
Это всё поделить на x, или только 1?
Ответы
Автор ответа:
1
С - на + - точка МИНИМУМА. Точки максимума - нету.
0,5 входит в интервал от [ 0,25 ; 1 ]
Ответ: 0,5
нет такого ответа в вариантах.Варианты:6,10 1/4, 7 1/4,8,9 1/4
Странно
Похожие вопросы
Предмет: Немецкий язык,
автор: kokich89
Предмет: Биология,
автор: dimonnx
Предмет: Математика,
автор: qbee4909
Предмет: Математика,
автор: Привет201881
Предмет: Математика,
автор: ульяна279