Предмет: Геометрия,
автор: phisicschemistry
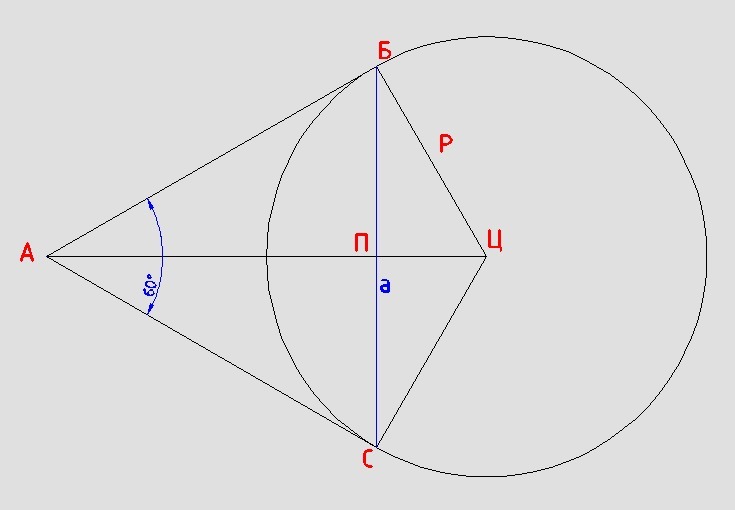
К окружности проведены касательные АВ и АС. В и С - точки касания. Чему равен радиус окружности, если угол А равен 60 градусов, ВС=а?
Ответы
Автор ответа:
0
∠БАЦ = ∠БАС/2 = 60/2 = 30°
∠АБЦ = 90°
∠БСП = ∠БЦА = 180 - 90 - 30 = 60°
В прямоугольном ΔПБЦ
∠ПБЦ = 180 - 90 - 60 = 30°
Катет ПЦ против этого угла в два раза меньше гипотенузы
БЦ = Р
ПЦ = Р/2
БП = а/2
По Пифагору
(а/2)² + (Р/2)² = Р²
а²/4 = 3Р²/4
а² = 3Р²
Р² = а²/3
Р = а/√3
∠АБЦ = 90°
∠БСП = ∠БЦА = 180 - 90 - 30 = 60°
В прямоугольном ΔПБЦ
∠ПБЦ = 180 - 90 - 60 = 30°
Катет ПЦ против этого угла в два раза меньше гипотенузы
БЦ = Р
ПЦ = Р/2
БП = а/2
По Пифагору
(а/2)² + (Р/2)² = Р²
а²/4 = 3Р²/4
а² = 3Р²
Р² = а²/3
Р = а/√3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Dmitrii9793
Предмет: Математика,
автор: altynbekgreat
Предмет: Алгебра,
автор: kareval921
Предмет: Алгебра,
автор: byms1