Предмет: Алгебра,
автор: 1nnnnnn11
Реши квадратное уравнение 2(10x−23)2−9(10x−23)+4=0
(первым вводи больший корень)
x1=; x2=
Дополнительный вопрос:
Какой метод рациональнее использовать?
Вынесение за скобку
Разложение на множители
Метод введения новой переменной
Раскрывание скобок
Ответы
Автор ответа:
0
Вот держи. У меня не получилось квадратної уравнение но получилось так.
Приложения:
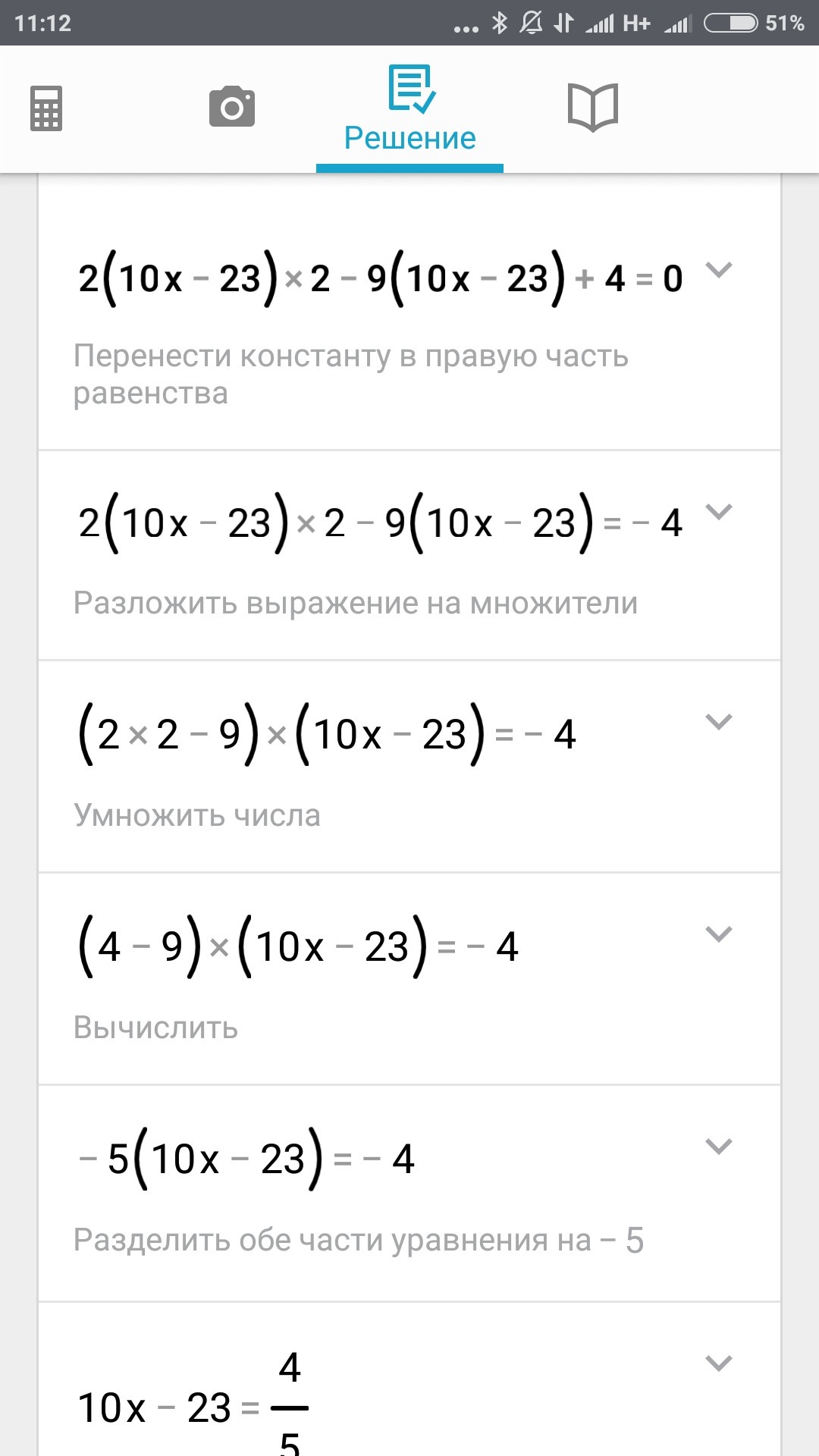
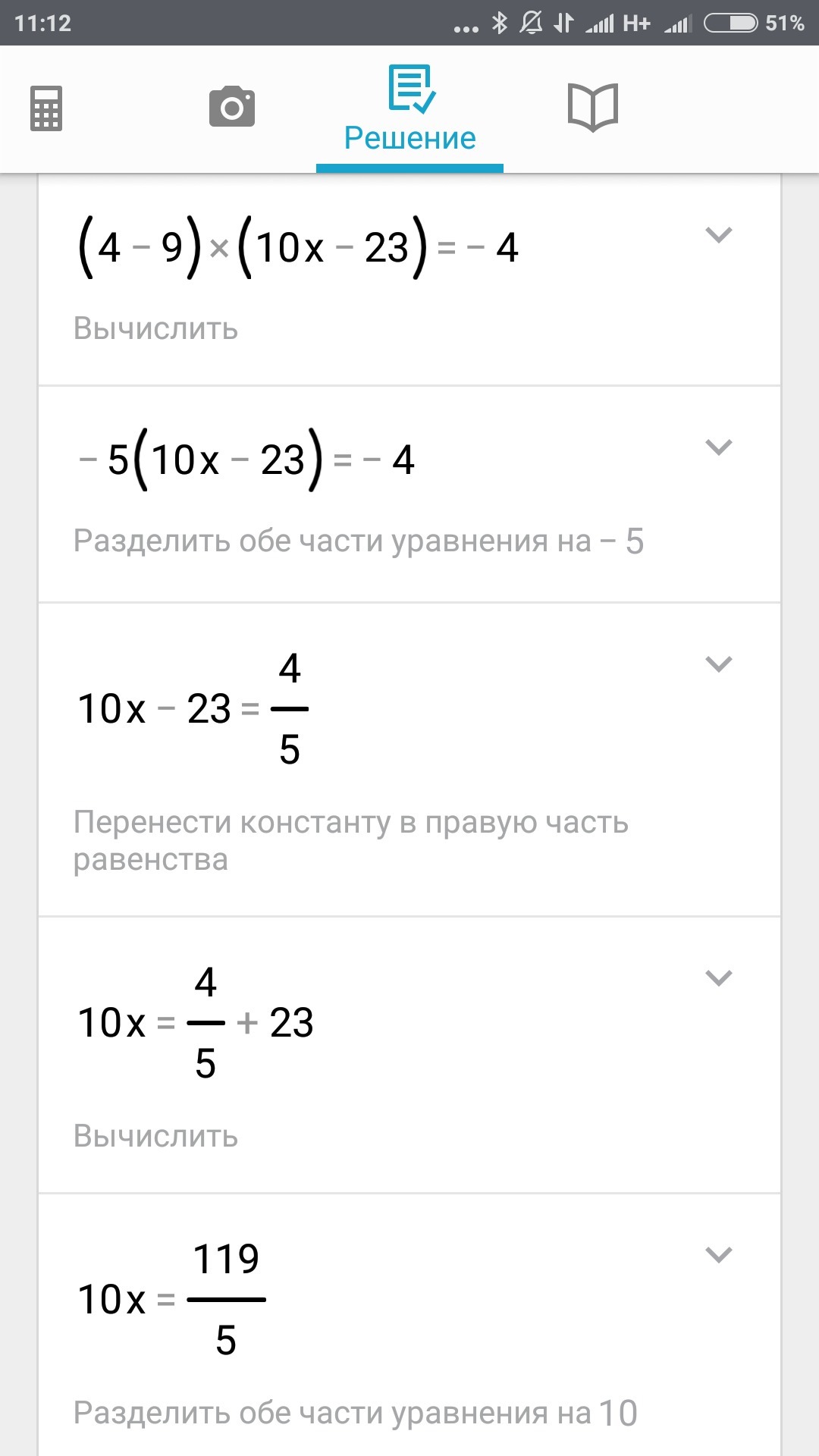
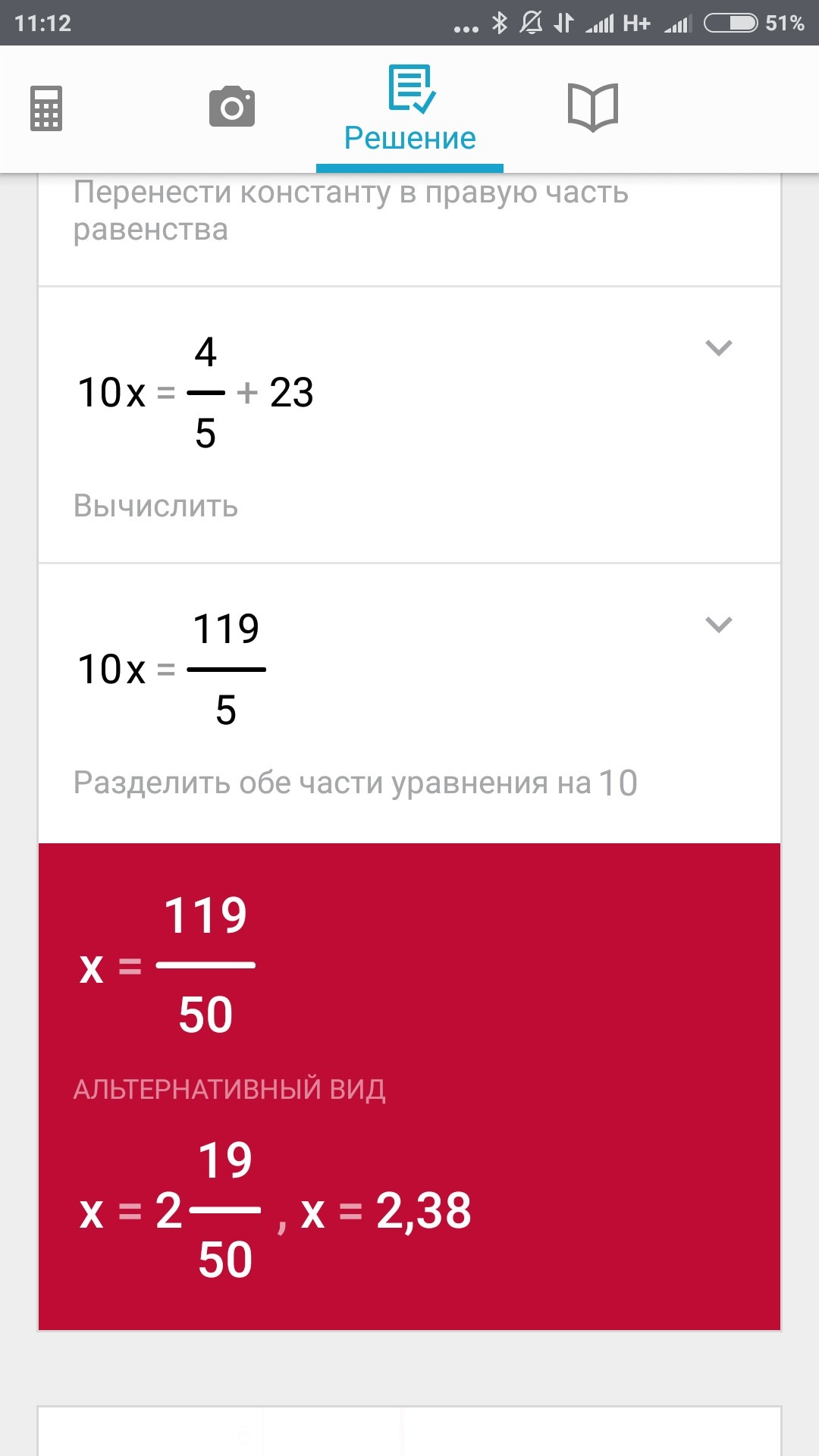
Автор ответа:
1
В данном случае рациональнее использовать "метод введения новой переменной"!
2(10x-23)^2 -9(10x-23) +4 = 0
Заменим (10х-23)=t, тогда
2t^2 -9t+4=0
D=81-32=49
t1=(9-7)/4=2/4=1/2
t2=(9+7)/4=16/4=4
10x-23=1/2
10x=1/2 +23
10x=23,5
x=23,5:10
x1=2,35
10x-23=4
10x=4+23
10x=27
x=27:10
x2=2,7
Ответ: х1=2,7 ; х2=2,35
2(10x-23)^2 -9(10x-23) +4 = 0
Заменим (10х-23)=t, тогда
2t^2 -9t+4=0
D=81-32=49
t1=(9-7)/4=2/4=1/2
t2=(9+7)/4=16/4=4
10x-23=1/2
10x=1/2 +23
10x=23,5
x=23,5:10
x1=2,35
10x-23=4
10x=4+23
10x=27
x=27:10
x2=2,7
Ответ: х1=2,7 ; х2=2,35
Похожие вопросы
Предмет: Математика,
автор: hellodog
Предмет: Литература,
автор: Whatisass
Предмет: Алгебра,
автор: irinapawlenko4
Предмет: Математика,
автор: nikkob14
Предмет: Математика,
автор: Julia0802