Question

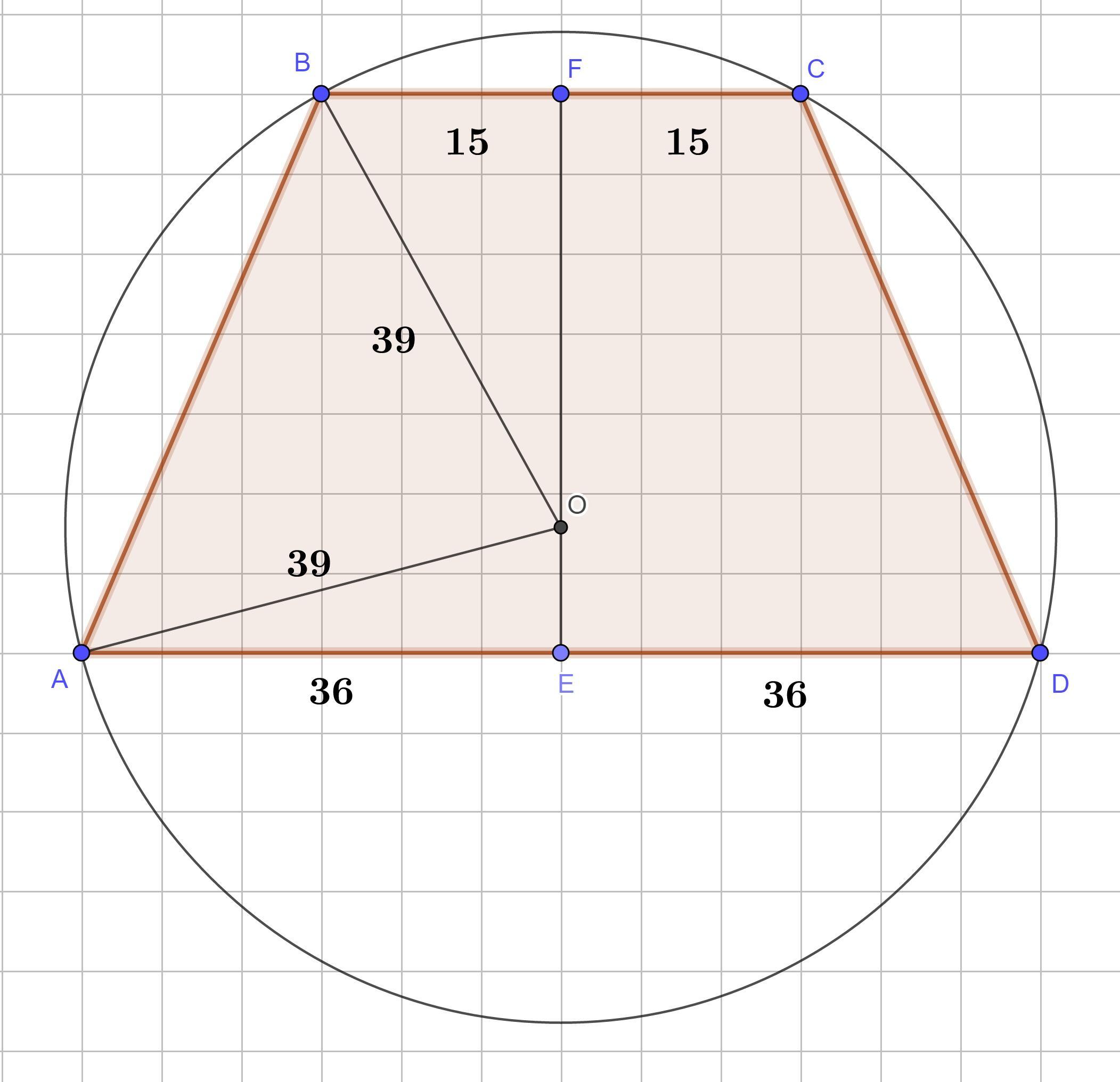
Основание равнобедренной трапеции равны 72 и 30. центр окружности описанной около трапеции лежит внутри трапеции а радиус окружности равен 39 Найдите высоту трапеции

Answer 1

Ответ:

Высота = 51

Пошаговое объяснение:

Пусть ABCD - трапеция (BC ║ AD), AB = CD (см. рисунок)

E, F - середины оснований, O - центр описанной окружности, O ∈ EF,  EF - высота трапеции.

Из ΔAOE (∠E = 90°) OE² = 39² - 36² = 3·75 = 9·25 ⇒ OE = 3·5 = 15 (по Теореме Пифагора)

Из ΔBOF (∠F = 90°) OF² = BO² - BF² = 39² - 15² = 24·54 = 4·6·6·9 ⇒ OF = 2·6·3 = 36 (по Теореме Пифагора)

EF = OE + OF = 15 + 36 = 51