Предмет: Математика,
автор: siri098
Срочно надо!!!!!!!!
Помогите пожалуйста решить
Приложения:
Ответы
Автор ответа:
2
1) Воспользуемся признаком перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна всей плоскости.
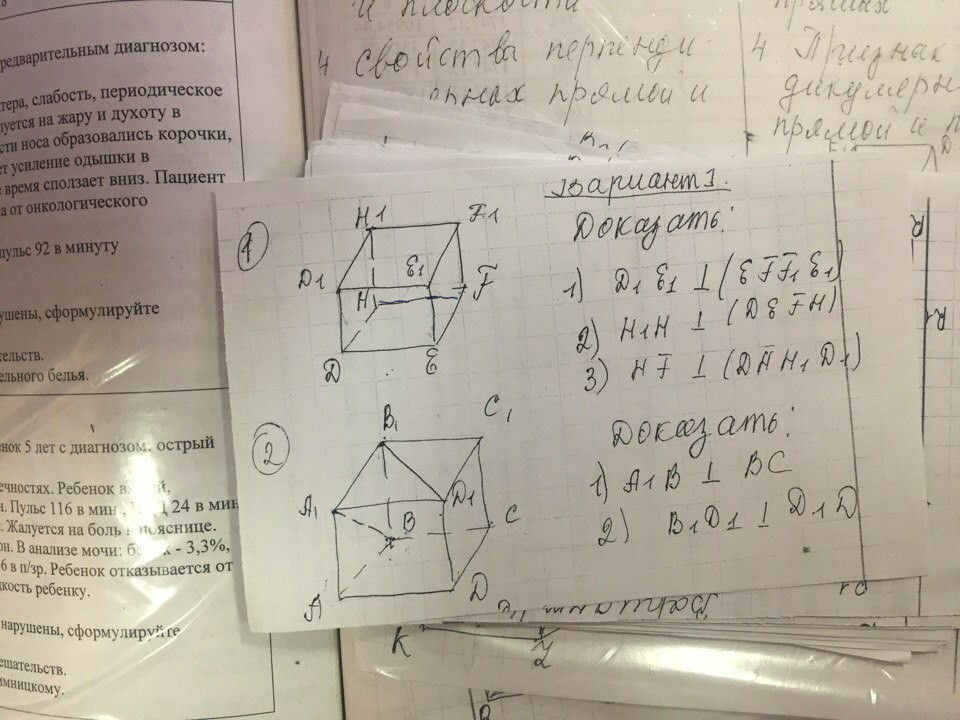
1) D₁E₁ ⊥ E₁F₁, D₁E₁ ⊥ EE₁ ⇒ D₁E₁ ⊥ (EFF₁E₁) доказано
2) H₁H ⊥ HD, H₁H ⊥ HF ⇒ H₁H ⊥ (DEFH) - доказано
3) HF ⊥ HD, HF ⊥ HH₁ ⇒ HF ⊥ (DHH₁D₁) - доказано
2) Воспользуемся определением перпендикулярности прямой и плоскости:
если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой в этой плоскости
1) BC ⊥ AB, BC⊥BB₁ ⇒ BC ⊥ (ABB₁A₁) ⇒ BC⊥A₁B - доказано
2) D₁D⊥ D₁A₁, D₁D⊥D₁C₁ ⇒ D₁D⊥ (A₁B₁C₁D₁) ⇒ D₁D⊥ B₁D₁ - доказано
1) D₁E₁ ⊥ E₁F₁, D₁E₁ ⊥ EE₁ ⇒ D₁E₁ ⊥ (EFF₁E₁) доказано
2) H₁H ⊥ HD, H₁H ⊥ HF ⇒ H₁H ⊥ (DEFH) - доказано
3) HF ⊥ HD, HF ⊥ HH₁ ⇒ HF ⊥ (DHH₁D₁) - доказано
2) Воспользуемся определением перпендикулярности прямой и плоскости:
если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой в этой плоскости
1) BC ⊥ AB, BC⊥BB₁ ⇒ BC ⊥ (ABB₁A₁) ⇒ BC⊥A₁B - доказано
2) D₁D⊥ D₁A₁, D₁D⊥D₁C₁ ⇒ D₁D⊥ (A₁B₁C₁D₁) ⇒ D₁D⊥ B₁D₁ - доказано
Похожие вопросы
Предмет: Русский язык,
автор: aynurqadirov561
Предмет: Химия,
автор: appol0n
Предмет: Физика,
автор: Аноним
Предмет: Литература,
автор: Dians11111