Предмет: Алгебра,
автор: viknest25
Помогите решить 3. б)
Приложения:
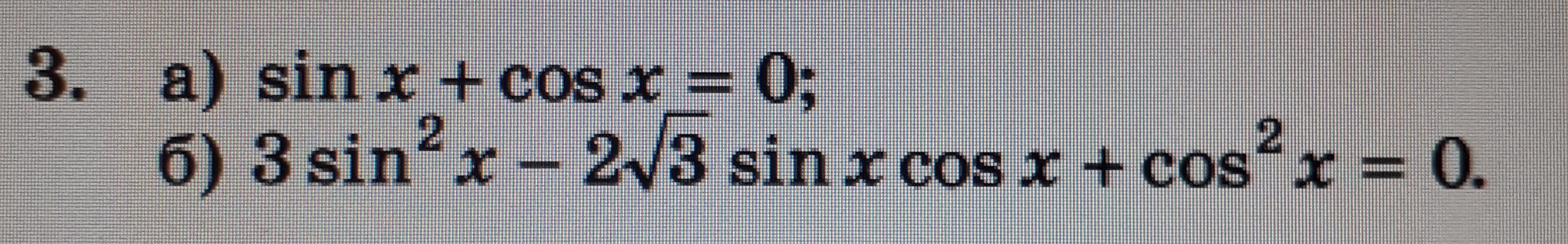
Ответы
Автор ответа:
2
Решение
3sin²x - 2√xsinxcosx + cos²x = 0
(√3sinx - cosx)² = 0
√3sinx - cosx = 0 делим на cosx ≠ 0, x ≠ π/2 + πk, k ∈ Z
√3tgx - 1 = 0
tgx = 1/√3
x = arctg(1/√3) + πn, n ∈ Z
x = π/6 + πn, n ∈ Z
3sin²x - 2√xsinxcosx + cos²x = 0
(√3sinx - cosx)² = 0
√3sinx - cosx = 0 делим на cosx ≠ 0, x ≠ π/2 + πk, k ∈ Z
√3tgx - 1 = 0
tgx = 1/√3
x = arctg(1/√3) + πn, n ∈ Z
x = π/6 + πn, n ∈ Z
Похожие вопросы
Предмет: Математика,
автор: vika2009kurbatova
Предмет: Математика,
автор: miklashmash
Предмет: Қазақ тiлi,
автор: nigaraa2007
Предмет: Математика,
автор: игнат2007
Предмет: География,
автор: asret2