Предмет: Алгебра,
автор: jasikprincess
50 БАЛЛОВ Помогите с любым номером, в первом задании при а=2, n=-1, c=-3
Приложения:

zhenyaM2002:
Обнови страницу- будут дроби.
Ответы
Автор ответа:
1
1.

при а = 2 ; n=-1 ; с = -3

2.

тождество доказано.
3. не видно знака ( х + 1 ??? 1/(х+1)) ...
при а = 2 ; n=-1 ; с = -3
2.
тождество доказано.
3. не видно знака ( х + 1 ??? 1/(х+1)) ...
Приложения:
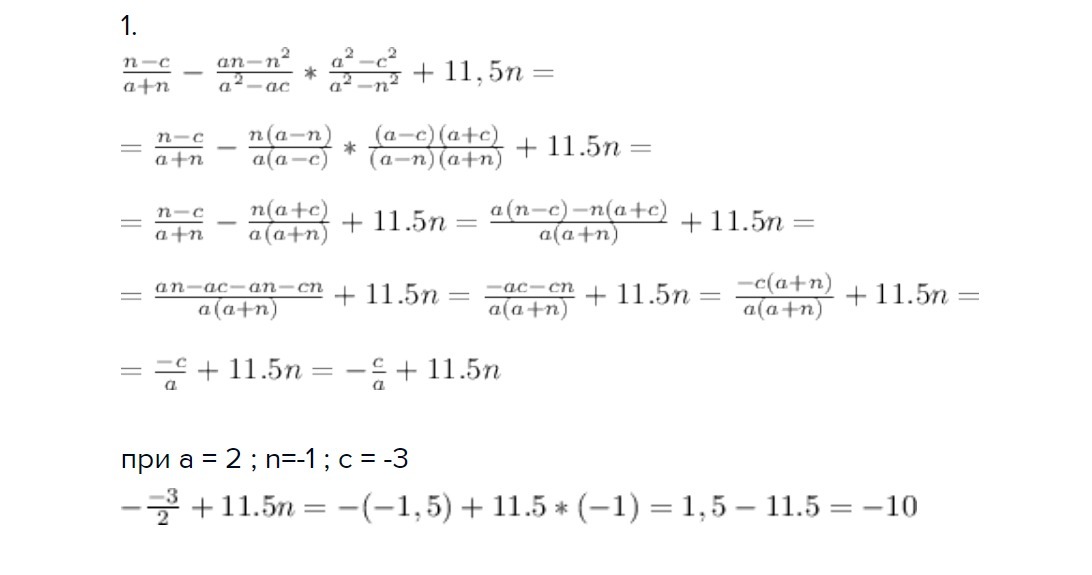

Какие-то знаки
Это фото было?
Обнови страницу- будут дроби)
Обновила
не изменилось
Срочно нужно
Странно... Нет в местном редакторе написал... Обычно обновляешь => он показывает дробь)))
Я их вижу.
Смотри приложение) Там то же, что и в ответе...
=>
Похожие вопросы
Предмет: Математика,
автор: HollyGenshin
Предмет: Физика,
автор: nassibyllinnNikita
Предмет: Математика,
автор: MTE626
Предмет: Математика,
автор: mila1983