Предмет: Математика,
автор: editor71
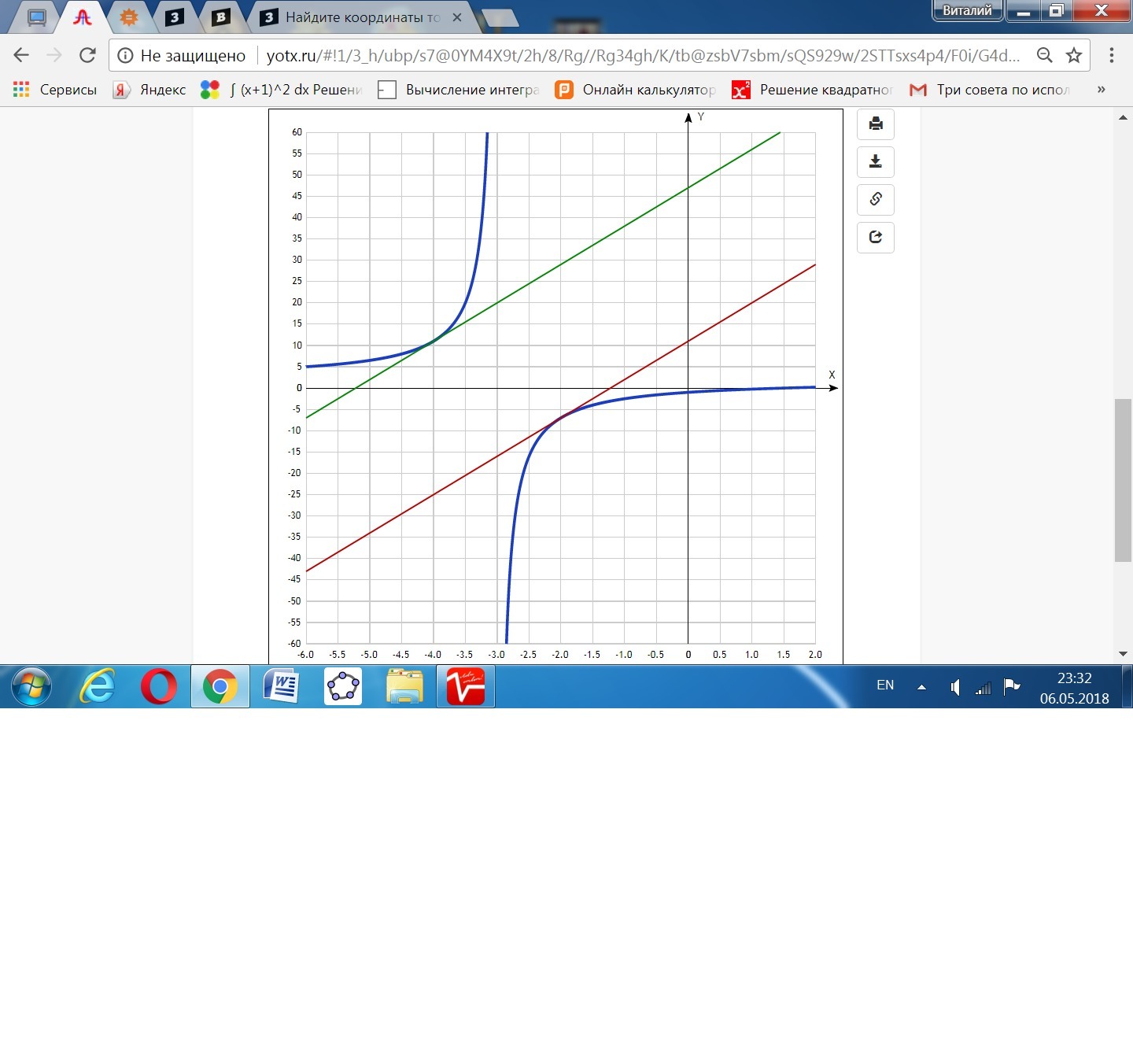
Найдите координаты точек пересечения с осями координат касательных к графику функции Y=(2x-3)/( x+3)
имеющих угловой коэффициент 9.
Ответы
Автор ответа:
6
Уравнение касательной у = y'(xo)*(x - xo) + y(xo).
Находим: у=(2x-3)/( x+3), y' = 9/(x+3)².
Приравниваем производную заданному в условии значению:
9/(x+3)² = 9. Отсюда видно, что знаменатель должен быть равен 1.
(x+3)² = 1.
х² + 6х + 9 = 1,
х² + 6х + 8 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*1*8=36-4*8=36-32=4;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√4-6)/(2*1)=(2-6)/2=-4/2=-2;x_2=(-√4-6)/(2*1)=(-2-6)/2=-8/2=-4.
Получили 2 точки касания хо1 = -2 и хо2 = -4.
Значения y'(хо) и y(xo) равны:
y'(хо1) = 9/(-2+3)² = 9, и y(xo1) = (2*(-2)-3)/(-2+3) = -7,
y'(хо2) = 9/(-4+3)²/(-4+3) = 9 и y(xo2) = (2*(-4)-3)/(-4+3) = 11.
Находим 2 уравнения касательных:
у1к = 9(х + 2) - 7 = 9х + 18 - 7 = 9х + 11.
у2к = 9(х + 4) + 11 = 9х + 36 + 11 = 9х + 47.
Теперь можно получить ответ:
х1 = 0, у1 = 11,
х2 = 0, у2 = 47.
у1 = 0 , x1 = -11/9,
y2 = 0, x2 = 47/9.
Находим: у=(2x-3)/( x+3), y' = 9/(x+3)².
Приравниваем производную заданному в условии значению:
9/(x+3)² = 9. Отсюда видно, что знаменатель должен быть равен 1.
(x+3)² = 1.
х² + 6х + 9 = 1,
х² + 6х + 8 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*1*8=36-4*8=36-32=4;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√4-6)/(2*1)=(2-6)/2=-4/2=-2;x_2=(-√4-6)/(2*1)=(-2-6)/2=-8/2=-4.
Получили 2 точки касания хо1 = -2 и хо2 = -4.
Значения y'(хо) и y(xo) равны:
y'(хо1) = 9/(-2+3)² = 9, и y(xo1) = (2*(-2)-3)/(-2+3) = -7,
y'(хо2) = 9/(-4+3)²/(-4+3) = 9 и y(xo2) = (2*(-4)-3)/(-4+3) = 11.
Находим 2 уравнения касательных:
у1к = 9(х + 2) - 7 = 9х + 18 - 7 = 9х + 11.
у2к = 9(х + 4) + 11 = 9х + 36 + 11 = 9х + 47.
Теперь можно получить ответ:
х1 = 0, у1 = 11,
х2 = 0, у2 = 47.
у1 = 0 , x1 = -11/9,
y2 = 0, x2 = 47/9.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: zuhrasahieva157
Предмет: Обществознание,
автор: pmmoll081
Предмет: История,
автор: lagunsofia2
Предмет: География,
автор: kylie1
Предмет: Математика,
автор: 9040022914