Предмет: Алгебра,
автор: иска4578
Выполните действия. Номер 41.1 2) 4) 6) пример. Тема Тождественные преобразования алгебраических выражений
Приложения:
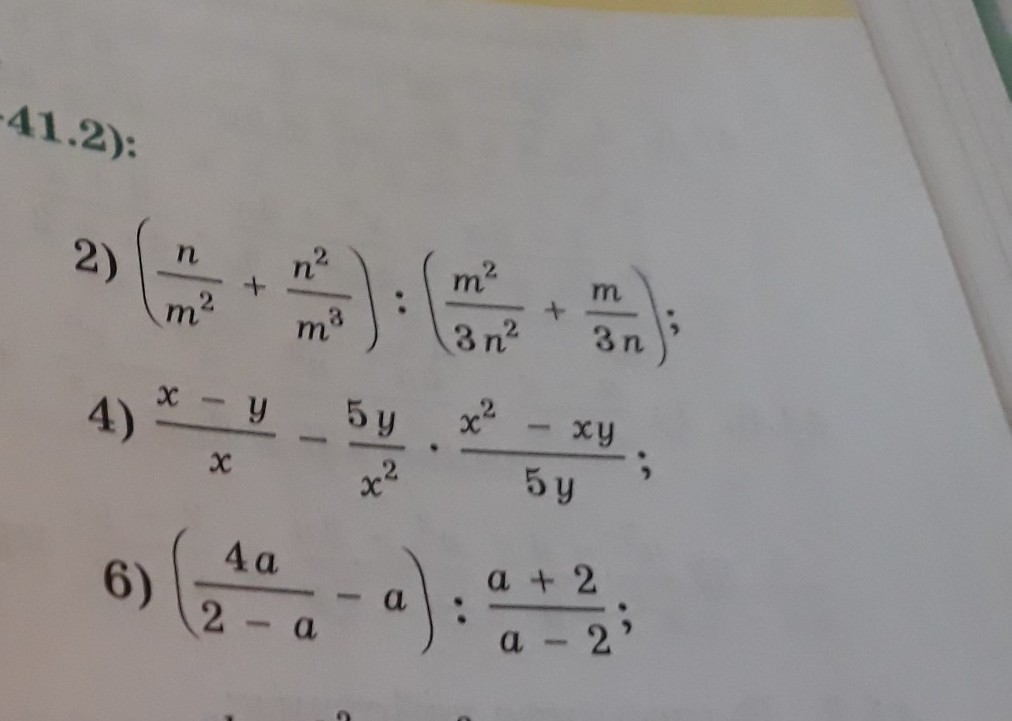
Ответы
Автор ответа:
108
Похожие вопросы
Предмет: Математика,
автор: evtelevizyon03
Предмет: Английский язык,
автор: Slavasherban1996
Предмет: Математика,
автор: chrisclawisthebest
Предмет: Алгебра,
автор: lolikum
Предмет: Математика,
автор: линамолния