Предмет: Геометрия,
автор: uratix
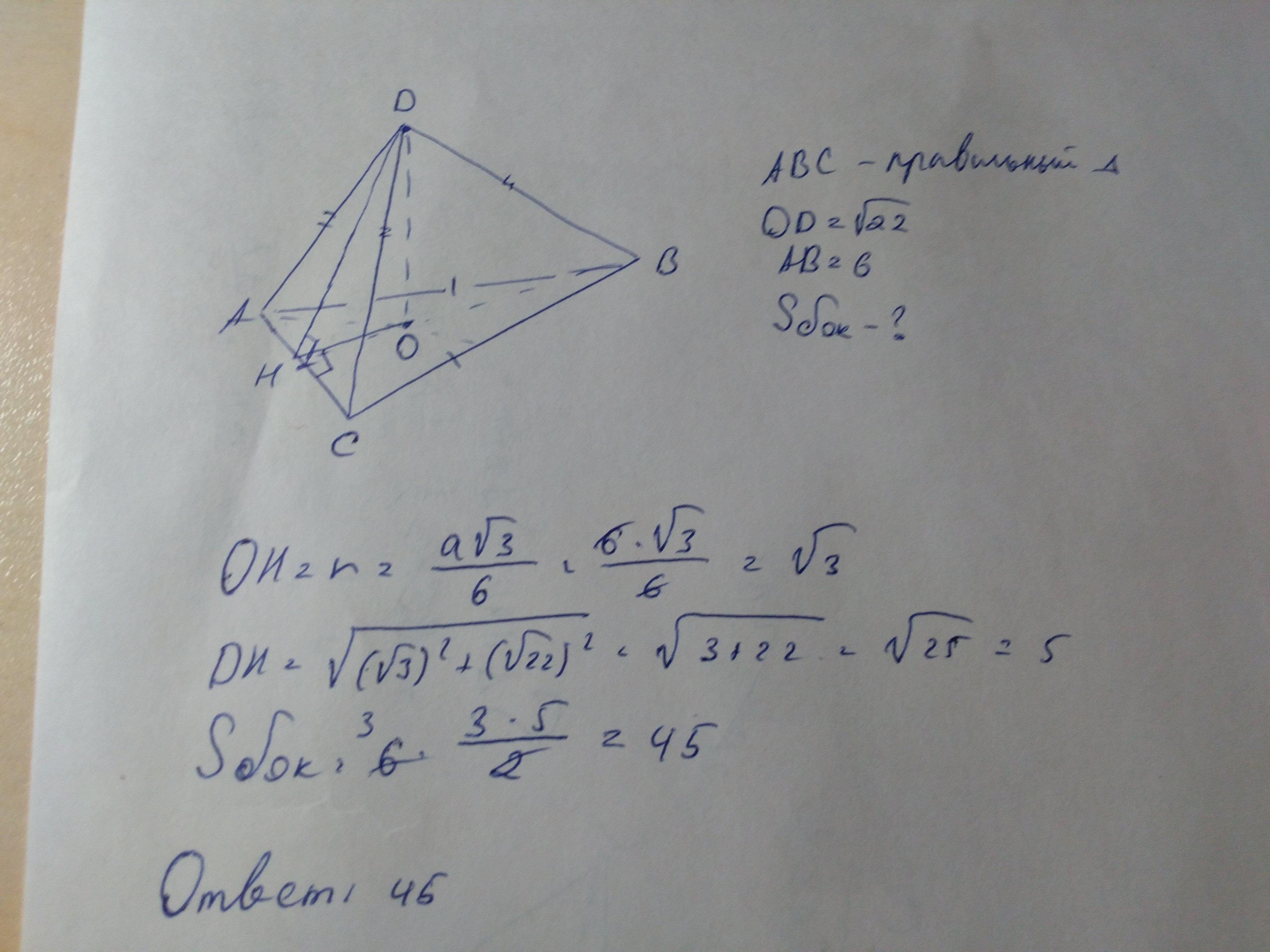
В правильной треугольной пирамиде сторона основания равна 6. Высота пирамиды равна корню из 22. найти площадь боковой поверхности пирамиды
Если можно, то с рисунком и подробным решением.
Ответы
Автор ответа:
5
В ΔABC проводим радиус вписанной окружности OH, в пирамиде - апофему DH.
ОH считаем по формуле радиуса вписанной в правильный треугольник окружности (r=a√3/6), по теореме Пифагора находим DH.
Площадь боковой поверхности пирамиды равна шести площадям прямоугольного треугольника DHC (св-во правильной пирамиды) с катетами HC=AC/2=3 и DH=5.
Ответ: 45
ОH считаем по формуле радиуса вписанной в правильный треугольник окружности (r=a√3/6), по теореме Пифагора находим DH.
Площадь боковой поверхности пирамиды равна шести площадям прямоугольного треугольника DHC (св-во правильной пирамиды) с катетами HC=AC/2=3 и DH=5.
Ответ: 45
Приложения:
Nastia4125:
Скажите пожалуйста откуда взяли корень из 3
Похожие вопросы
Предмет: Английский язык,
автор: zannaepiseva65
Предмет: Физика,
автор: fan94
Предмет: Українська мова,
автор: Аноним
Предмет: Информатика,
автор: вика1490
Предмет: Физика,
автор: вадим375