Предмет: Алгебра,
автор: polinaa1999
Помогите пожалуйста
С подробным решением
Приложения:
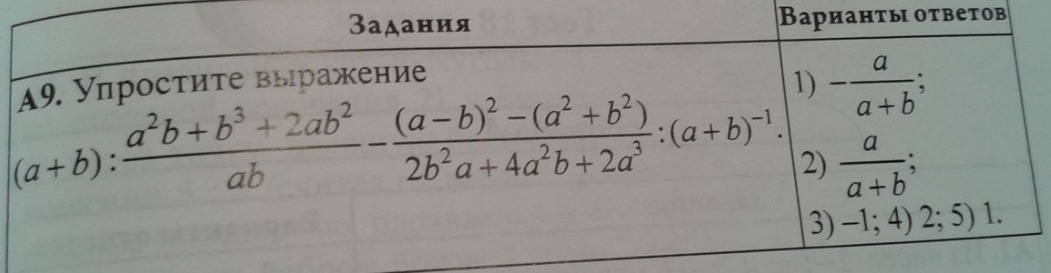
Ответы
Автор ответа:
1
А9

Ответ: 5
Ответ: 5
Похожие вопросы
Предмет: Русский язык,
автор: arslan81
Предмет: Алгебра,
автор: timofejsmirnov59
Предмет: Физика,
автор: kykkikl
Предмет: Химия,
автор: mashulyazvereva
Предмет: Биология,
автор: 97899yjj