Question

РЕШИТЕ СРОЧНО ДАЮ 98 БАЛЛОВ.
№1
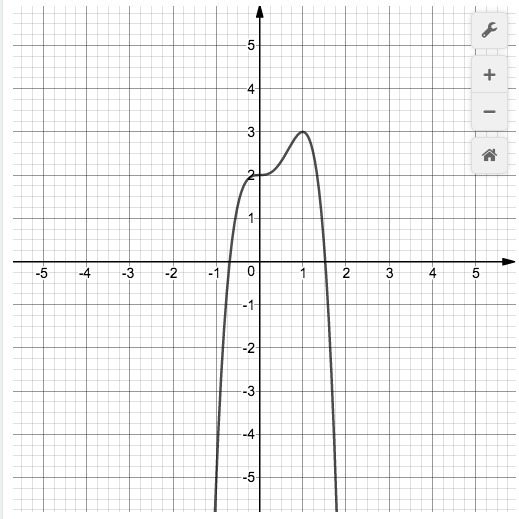
Найдите у наиб и у наим на интервале [0;+∞]
№2
Найдите наибольшее и наименьшее значения заданной функции на заданном интервале:
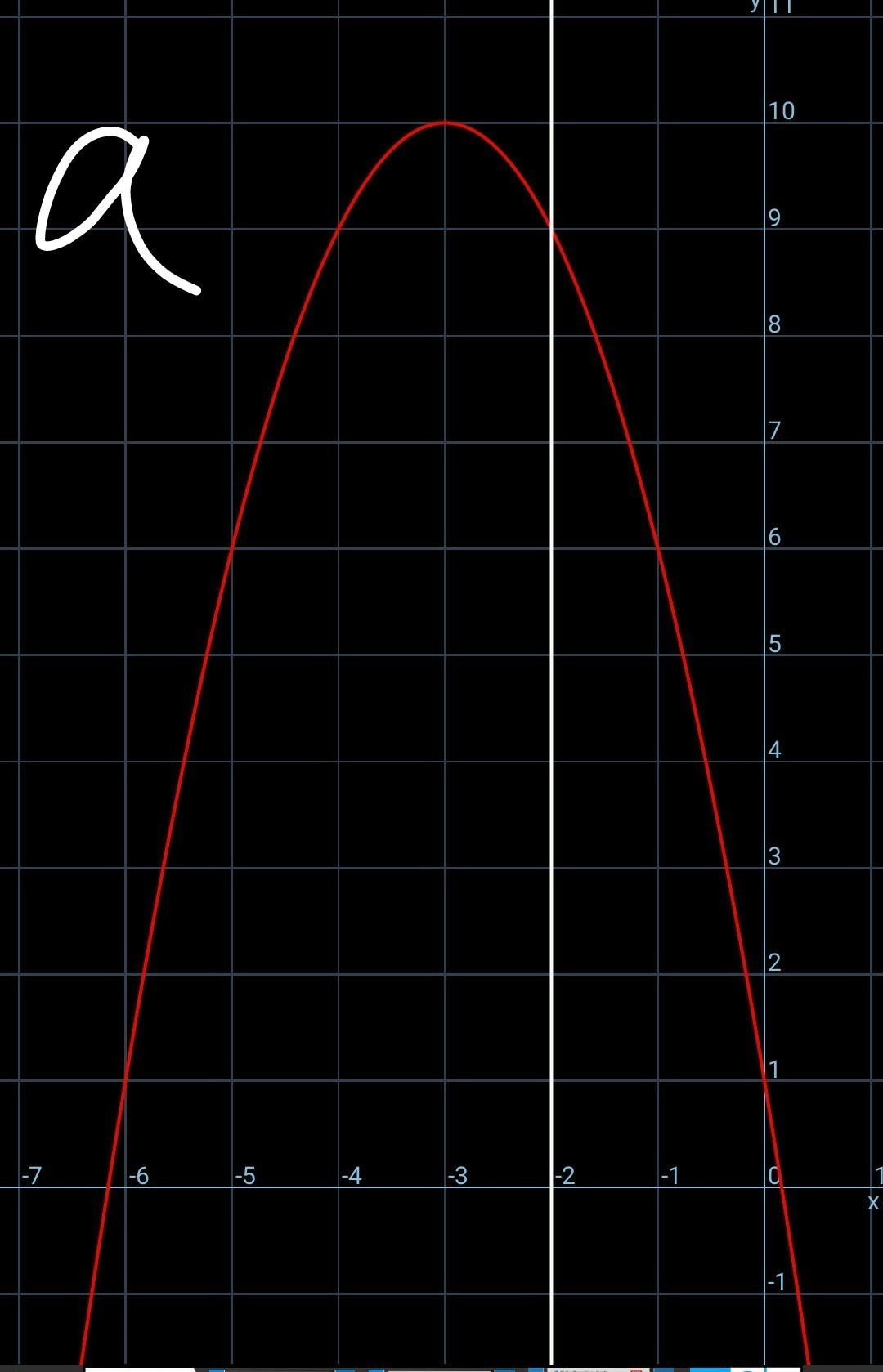
а)y=-x^2 - 6x + 1 на (-∞;-2]
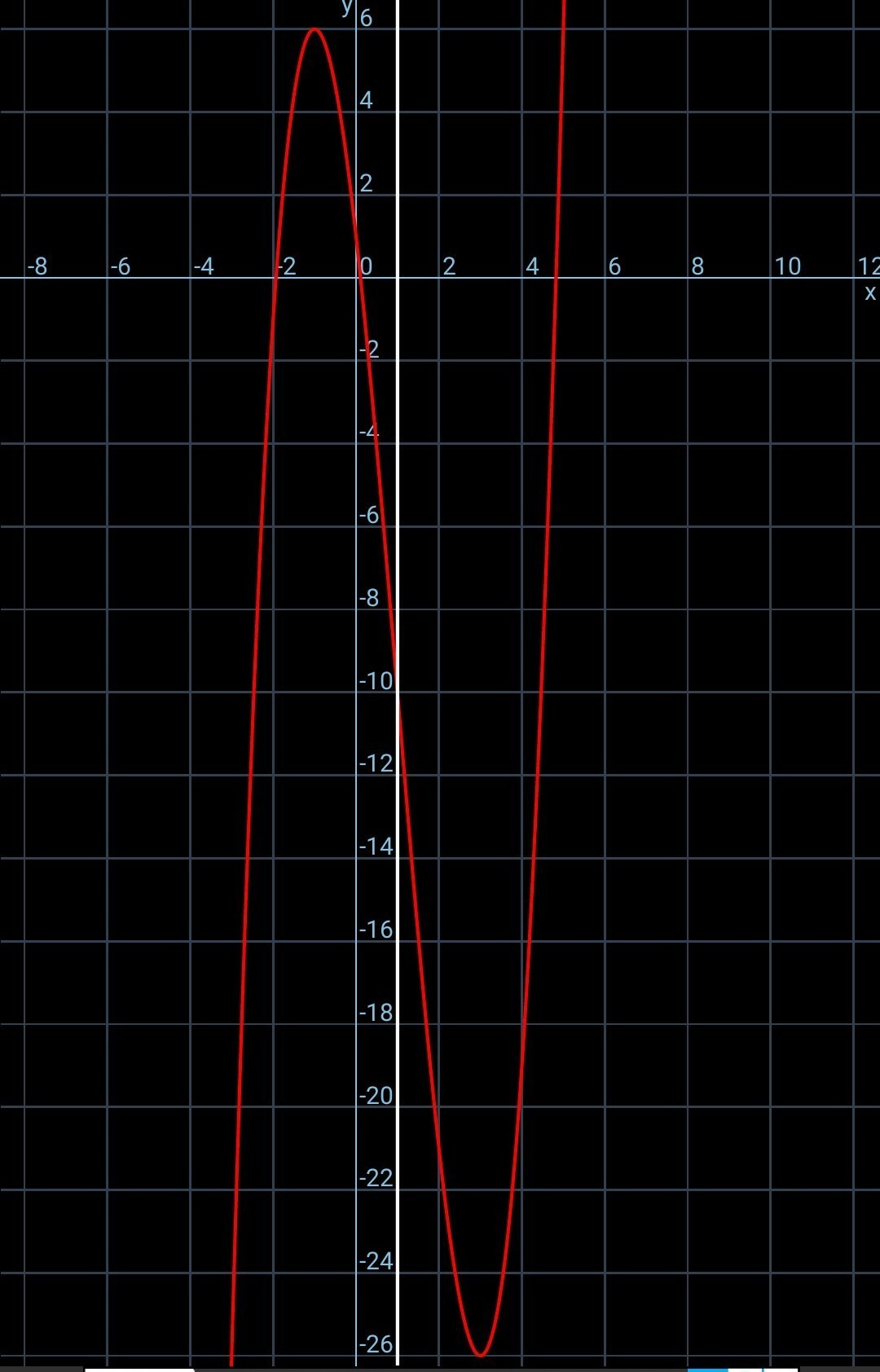
б)y=x^3 - 3x^2 - 9x + 1 на [1;+∞)

Answer 1

по графику данному на рисунке можно было ответить что функция имеет экстремум в точке (1;3) и это является ее максимальным значением.
Так как так как функция убывает с точки 1 до бесконечности то минимальное значение равно -∞
№1 - y min = -∞, y max = 3.

2.а) По графику видно что Ymax(-3) = - (-3)² - 6(-3) + 1 = 10
Ymin = -∞

2.б) Ymin(3) = 3³ - 3*3² - 9*3 + 1 = -26
Ymax = +∞