Предмет: Алгебра,
автор: azizef00p7xkpg
x^8 + 4x^2 + 4
Требуется разложить данный многочлен с решением ОБЯЗАТЕЛЬНО. Буду проверять решение. Не срочно. Если его невозможно разложить, хочу видеть подробное доказательство
Приложения:
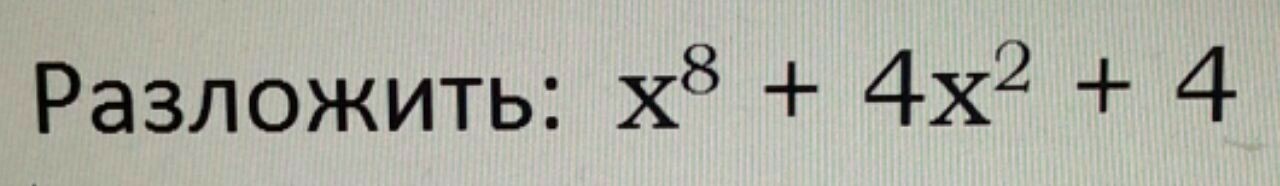
azizef00p7xkpg:
Прошу администрацию, к кому можно обратится с помощью? Есть кто может решить эту задачу? На сайте есть такие? Если нет, прошу вернуть мои балля
*баллы
очевидно, что у многочлена действительных корней нет, есть только мнимые.
Но ведь решение гарантируется, следовательно РАЗРЕШАЕТСЯ разложение любыми ЗАКОННЫМИ способами
Ответы
Автор ответа:
3
Самый быстрый способ разложить на множители с помощью формулы разности квадратов
x⁸ + 4x² + 4 =

Задача выполнена. Многочлен разложен на произведение комплексных чисел. На этом можно было бы и закончить, потому как в условии ничего не сказано, на какие множители нужно раскладывать.
Но следом возможен вопрос о разложении на множители без использования мнимой единицы.Такое разложение не будет столь простым.
Предположим, что данный многочлен можно представить опять же в виде разности квадратов двух многочленов.
x⁸ + 4x² + 4 =
= (x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)²
Добавлять во вторую скобку слагаемое x⁴ и свободный член нецелесообразно, так как при возведении первой скобки в квадрат
(x⁴)² = x⁸ и 2² = 4
Итак, используя формулу квадрата суммы, раскроем скобки:
(x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)² =
= x⁸ + a²x⁶ + b²x⁴ + c²x² + 4 + 2ax⁷ + 2bx⁶ + 2cx⁵ + 4x⁴ +
+ 2abx⁵ + 2acx⁴ + 4ax³ + 2bcx³ + 4bx² + 4cx -
- m²x⁶ - n²x⁴ - p²x² - 2mnx⁵ - 2mpx⁴ - 2npx³ =
= x⁸ + 2ax⁷ + (a² + 2b - m²)x⁶ + (2c +2ab -2mn)x⁵ +
+ (b² + 4 + 2ac - n² - 2mp)x⁴ + (4a + 2bc - 2np)x³ +
+ (c² + 4b - p²)x² + 4cx + 4 =
= x⁸ + 4x² + 4
Коэффициенты при одинаковых степенях должны быть равны.
2ax⁷ = 0x⁷ ⇒ a = 0
4cx = 0x ⇒ c = 0
(a² + 2b - m²)x⁶ = 0x⁶ ⇒ 2b = m²
(4a + 2bc - 2np)x³ = 0x³ ⇒ np = 0
(2c + 2ab - 2mn)x⁵ = 0x⁵ ⇒ mn = 0
(b² + 4 + 2ac - n² - 2mp)x⁴ = 0x⁴ ⇒ b² + 4 = n² + 2mp
(c² + 4b - p²)x² = 4x² ⇒ 4b = p² + 4
np = 0 и mn = 0 Пусть n = 0. Тогда остаётся система из трёх уравнений с тремя неизвестными
1) 2b = m²
2) 4b = p² + 4
3) b² + 4 = 2mp
Решением этой системы являются b = m = p = 2
x⁸ + 4x² + 4 =
= (x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)² =
= (x⁴ + 2x² +2)² - (2x³ + 2x)² =
= (x⁴ + 2x² + 2 + 2x³ + 2x)(x⁴ + 2x² + 2 - 2x³ - 2x)
Ответ: возможные варианты разложения на множители
x⁸ + 4x² + 4 =
x⁸ + 4x² + 4 = (x⁴ + 2x² + 2 + 2x³ + 2x)(x⁴ + 2x² + 2 - 2x³ - 2x)
x⁸ + 4x² + 4 =
Задача выполнена. Многочлен разложен на произведение комплексных чисел. На этом можно было бы и закончить, потому как в условии ничего не сказано, на какие множители нужно раскладывать.
Но следом возможен вопрос о разложении на множители без использования мнимой единицы.Такое разложение не будет столь простым.
Предположим, что данный многочлен можно представить опять же в виде разности квадратов двух многочленов.
x⁸ + 4x² + 4 =
= (x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)²
Добавлять во вторую скобку слагаемое x⁴ и свободный член нецелесообразно, так как при возведении первой скобки в квадрат
(x⁴)² = x⁸ и 2² = 4
Итак, используя формулу квадрата суммы, раскроем скобки:
(x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)² =
= x⁸ + a²x⁶ + b²x⁴ + c²x² + 4 + 2ax⁷ + 2bx⁶ + 2cx⁵ + 4x⁴ +
+ 2abx⁵ + 2acx⁴ + 4ax³ + 2bcx³ + 4bx² + 4cx -
- m²x⁶ - n²x⁴ - p²x² - 2mnx⁵ - 2mpx⁴ - 2npx³ =
= x⁸ + 2ax⁷ + (a² + 2b - m²)x⁶ + (2c +2ab -2mn)x⁵ +
+ (b² + 4 + 2ac - n² - 2mp)x⁴ + (4a + 2bc - 2np)x³ +
+ (c² + 4b - p²)x² + 4cx + 4 =
= x⁸ + 4x² + 4
Коэффициенты при одинаковых степенях должны быть равны.
2ax⁷ = 0x⁷ ⇒ a = 0
4cx = 0x ⇒ c = 0
(a² + 2b - m²)x⁶ = 0x⁶ ⇒ 2b = m²
(4a + 2bc - 2np)x³ = 0x³ ⇒ np = 0
(2c + 2ab - 2mn)x⁵ = 0x⁵ ⇒ mn = 0
(b² + 4 + 2ac - n² - 2mp)x⁴ = 0x⁴ ⇒ b² + 4 = n² + 2mp
(c² + 4b - p²)x² = 4x² ⇒ 4b = p² + 4
np = 0 и mn = 0 Пусть n = 0. Тогда остаётся система из трёх уравнений с тремя неизвестными
1) 2b = m²
2) 4b = p² + 4
3) b² + 4 = 2mp
Решением этой системы являются b = m = p = 2
x⁸ + 4x² + 4 =
= (x⁴ + ax³ + bx² + cx +2)² - (mx³ + nx² + px)² =
= (x⁴ + 2x² +2)² - (2x³ + 2x)² =
= (x⁴ + 2x² + 2 + 2x³ + 2x)(x⁴ + 2x² + 2 - 2x³ - 2x)
Ответ: возможные варианты разложения на множители
x⁸ + 4x² + 4 =
x⁸ + 4x² + 4 = (x⁴ + 2x² + 2 + 2x³ + 2x)(x⁴ + 2x² + 2 - 2x³ - 2x)
Отличная работа! Это была олимпиадная задача, при чем олимпиада проходила для всех, кто увлекается математикой как наукой. Туда съехались со всей столицы. И я не встретил там человека который смог разложить. Олимпиада проходила для любых учащихся 10-11х классов или колледжей или лицеев
Похожие вопросы
Предмет: Математика,
автор: markejsksk
Предмет: Русский язык,
автор: evgenygarbuz99
Предмет: Математика,
автор: sasa0403
Предмет: Литература,
автор: 5050251
Предмет: Математика,
автор: саша1335