Предмет: Геометрия,
автор: 777noname111
В равнобедренном треугольнике АВС ( АВ = ВС ) угол при вершине В равен 120 градусов, СМ - биссектриса, АМ = 14 см. Найти расстояние от точки М до прямой ВС
Ответы
Автор ответа:
1
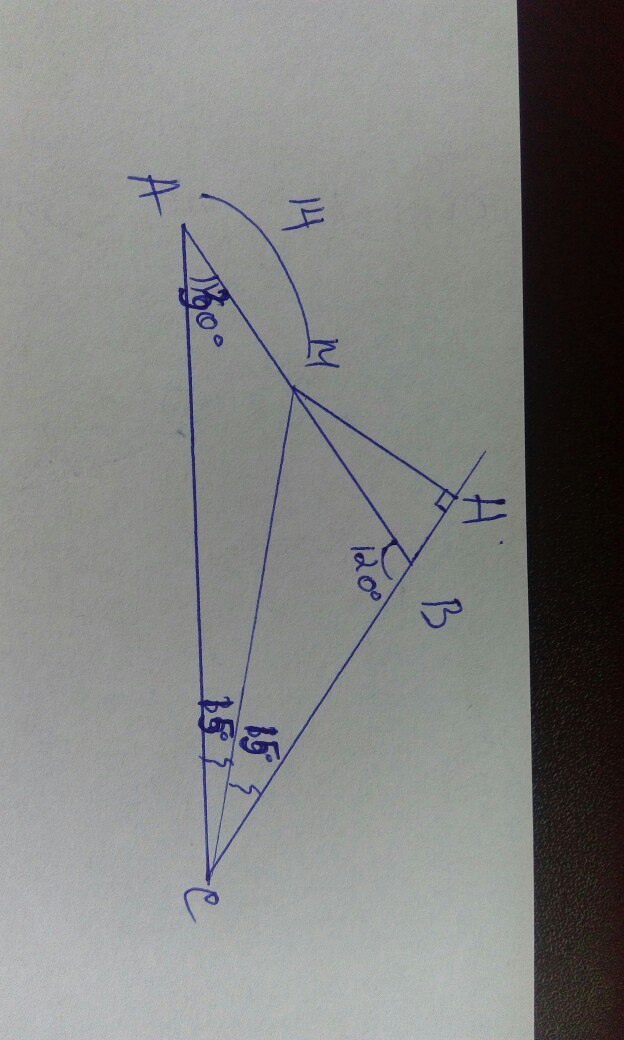
Рисунок к задаче оставлю ниже.
Решение. Так как треугольник АВС равнобедренный по условию и ∠ABC = 120°, то ∠BAC = ∠BCA = (180°-120°)/2 = 30°. Так как CM - биссектриса треугольника АВС, то ∠MCA = ∠ BCM = 15°.
Рассмотрим треугольник AMC. Из теоремы синусов: MC/sin30° = AM/sin15°. Выразим из пропорции длину стороны MC: MC = AM*sin30°/sin15° = 14*0,5/sin15° = 7/sin15° (см).
Пусть MH - перпендикуляр, проведенный из точки М к прямой ВС. Отрезок MH - искомое расстояние.
Рассмотрим треугольник МНС. ∠МНС = 90°, ∠НСМ = 15°. Выразим из этого треугольника длину катета МН: МН = MC*sin15° = 7*sin15°/sin15° = 7 (см).
Ответ: 7 см.
Решение. Так как треугольник АВС равнобедренный по условию и ∠ABC = 120°, то ∠BAC = ∠BCA = (180°-120°)/2 = 30°. Так как CM - биссектриса треугольника АВС, то ∠MCA = ∠ BCM = 15°.
Рассмотрим треугольник AMC. Из теоремы синусов: MC/sin30° = AM/sin15°. Выразим из пропорции длину стороны MC: MC = AM*sin30°/sin15° = 14*0,5/sin15° = 7/sin15° (см).
Пусть MH - перпендикуляр, проведенный из точки М к прямой ВС. Отрезок MH - искомое расстояние.
Рассмотрим треугольник МНС. ∠МНС = 90°, ∠НСМ = 15°. Выразим из этого треугольника длину катета МН: МН = MC*sin15° = 7*sin15°/sin15° = 7 (см).
Ответ: 7 см.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: lolokik85
Предмет: Математика,
автор: Lambburak
Предмет: Алгебра,
автор: onlymepizda
Предмет: Математика,
автор: зимакос
Предмет: Физика,
автор: Аноним