Question

исследовать на экстремум функцию y=x^3/x-4
PS x^3 (икс в кубе)

Answer 1

Дана функция  y=x³/(x-4).
Её производная y' = (2x²(x - 6))/((x - 4)²).
Отсюда видно, что она равна нулю при х = 0 и х = 6.
Найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена. На промежутках находят знаки производной.
Где производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Находим знаки производной:
х =    -1          0              1            6                7
у' = -0,56       0       -1,11111        0         10,88889.
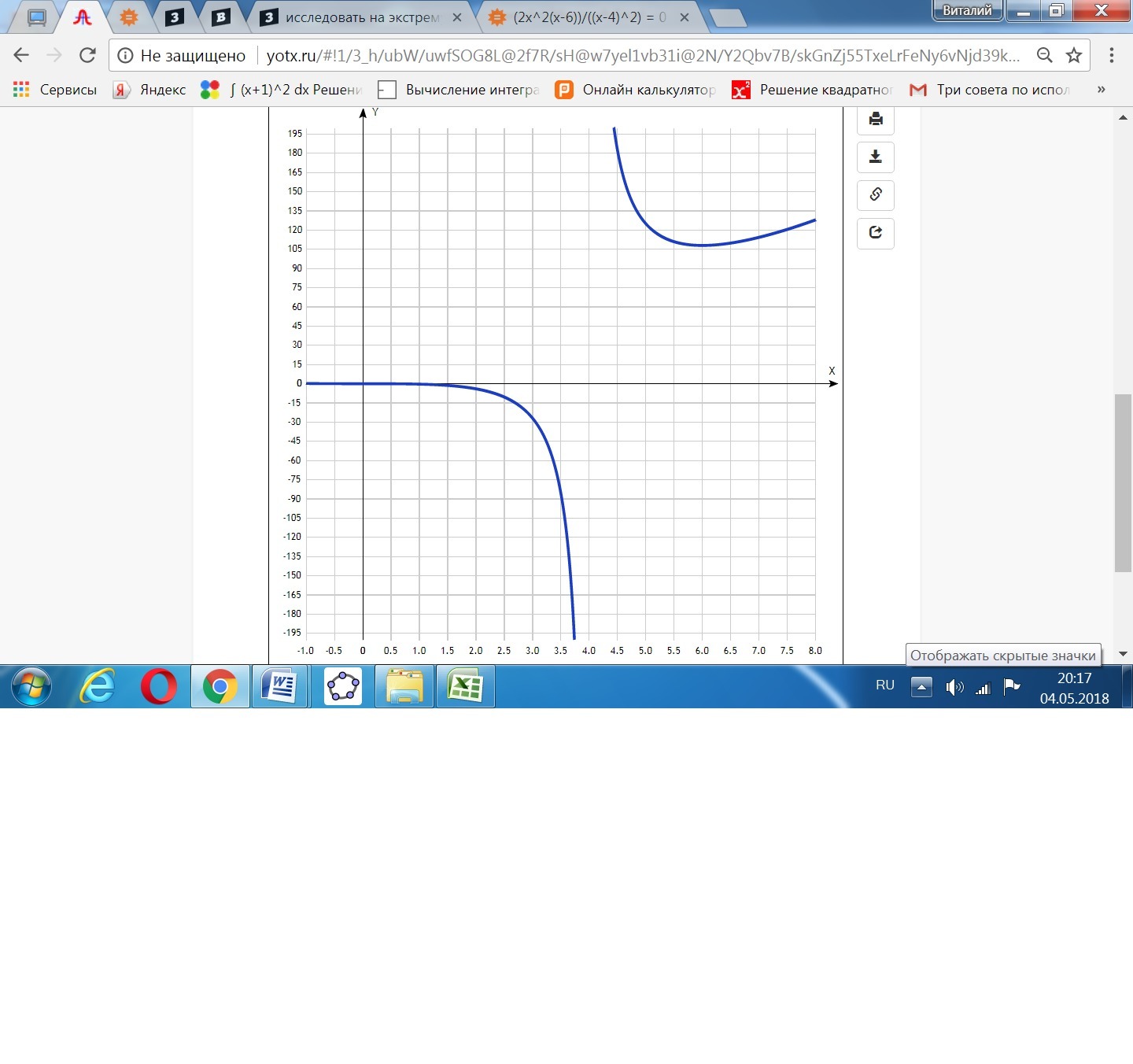
Как видим, критических точек две. а экстремум один - минимум в точке х = 6. у(6) = 108.
В точке х = 0 перегиб графика.