Question

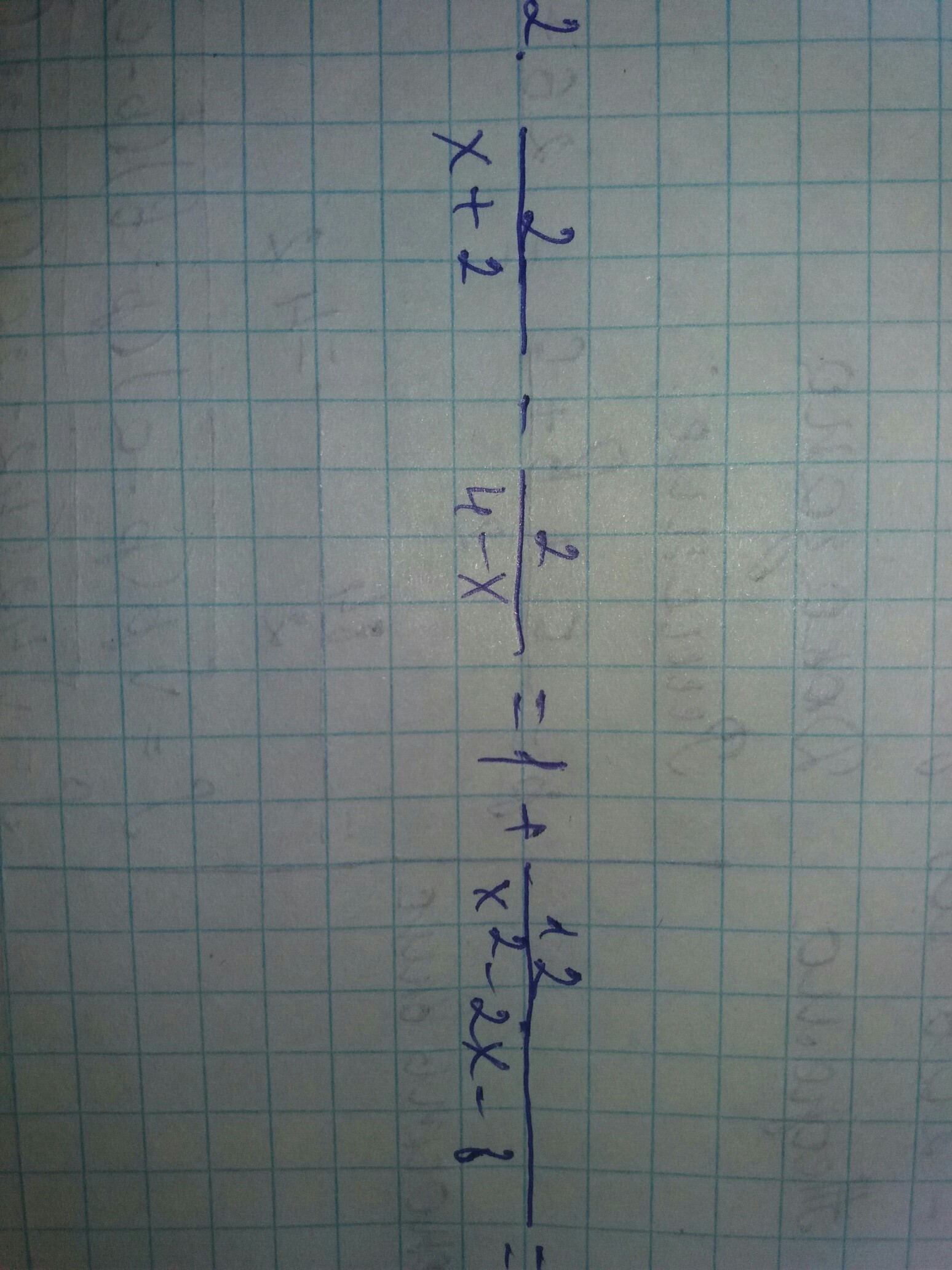
помогите решить пример по алгебре

Answer 1

$\frac{2}{x+2} - \frac{2}{4-x} = 1+ \frac{12}{x^2-2x - 8} \\ \\ \frac{2(4-x) - 2(x+2)}{(x+2)(4-x)} = \frac{x^2 - 2x - 8 + 12}{x^2-2x+1^2 - 9)} \\ \\ \frac{8 - 2x - 2x - 4}{(x+2)(4-x)} = \frac{x^2 -2x + 4}{(x-1)^2 - 3^2} \\ \\ \frac{4 - 4x}{(x+2)(4-x)} = \frac{(x^2-2x+4}{(x-1-3)(x-1+3)} \\ \\ \frac{-(4x-4)}{-(x-4)(x+2)} = \frac{x^2-2x+4}{(x-4)(x+2)} \\ \\ \frac{4x-4}{(x-4)(x+2)} = \frac{x^2-2x+4}{(x-4)(x+2)}$

Знаменатели дробей не должны быть равны 0 :
х + 2≠ 0 ;  х ≠ - 2
x - 4 ≠ 0 ;  х ≠ 4
Избавимся от знаменателей, умножим обе части уравнения
на (х - 4)(х + 2) :
4x - 4 = x² - 2x + 4
х²  - 2х  + 4  - 4х  + 4  = 0
х²  - 6х  + 8  = 0
D = (-6)²   - 4*1*8 =  36 - 32  = 4 = 2²
D> 0  -  два корня уравнения
х₁ = ( - (-6)  - 2)/(2*1) = (6 - 2)/2  = 4/2  = 2 
х₂ = ( - (-6) + 2)/(2*1) = (6+2)/2 = 8/2 = 4  не удовл. условию  (х≠4)

Ответ :  х = 2.