Предмет: Алгебра,
автор: kisheevap
Пожалуйста, помогите решить
Очень срочно
Приложения:
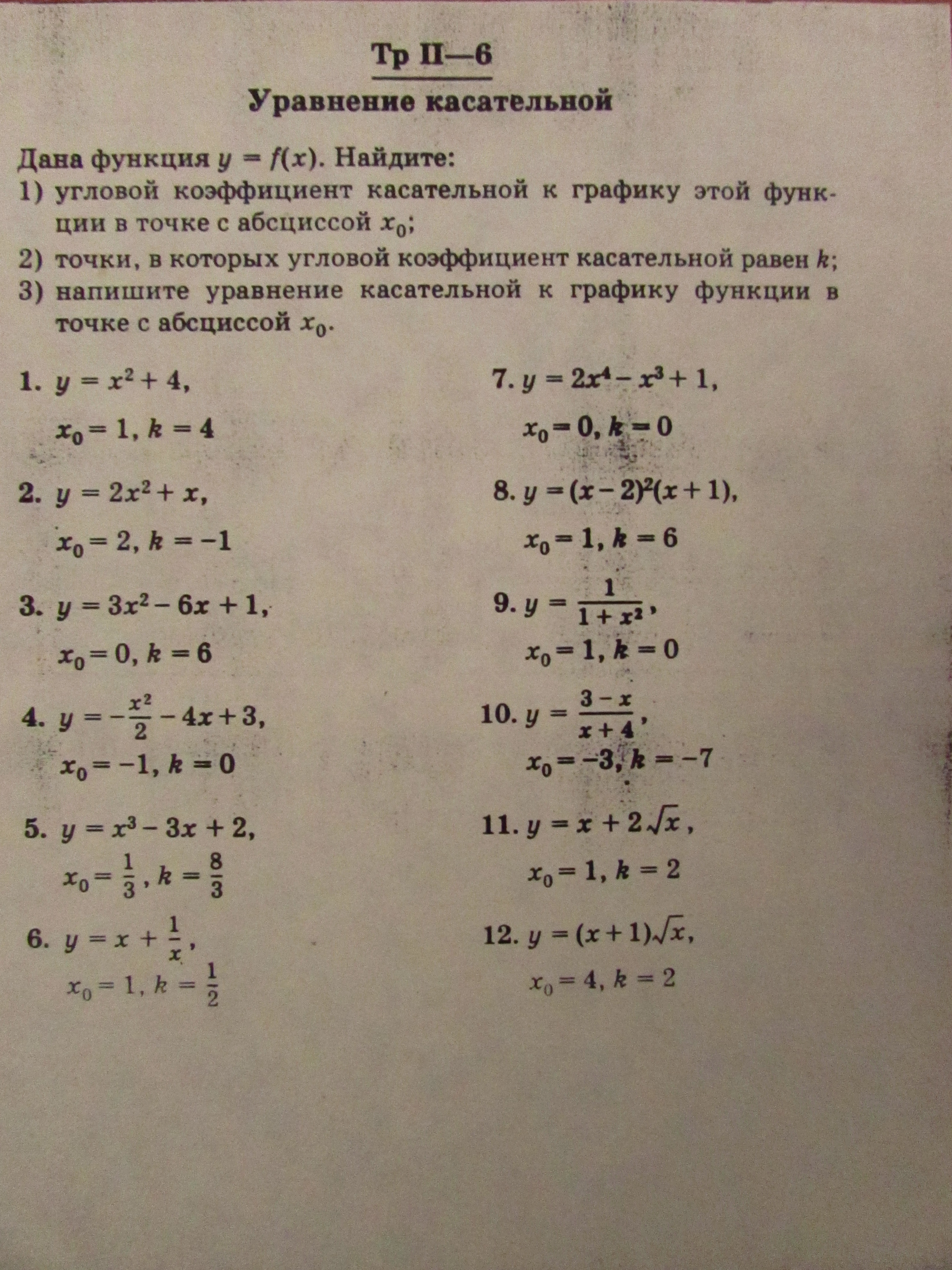
SweetBlackberry:
А вы сам принцип не понимаете? Я могу написать, как делать, и решить пару пунктов, но 12 - много
Была бы очень благодарна
Ответы
Автор ответа:
0
Уравнение касательной: y = f'(x0)(x - x0) + f(x0), где x0 - точка касания, f'(x0) - производная в точке касания.
Угловой коэффициент касательной - это f'(x0). Это все, что нужно знать, чтобы решить.
1) y = x² + 4
Чтобы найти значение производной в точке касания, найдем саму производную и подставим в нее абсциссу этой точки.
f'(x) = 2x
f'(x0) = 2 - угловой коэффициент.
Угловой коэффициент равен k: 2x = 4, x = 2.
Уравнение касательной к графику в точке с абсциссой x0: y = 2(x - 1) + 5, y = 2x + 3.
2) f'(x) = 4x + 1
f'(x0) = 9 - угловой коэффициент.
f'(x0) = - 1, если 4x + 1 = -1, x = -0.5.
Уравнение касательной: y = 9x - 18 + 10, y = 9x - 8.
3) f'(x) = 6x - 6
f(x0) = -6 - угловой коэффициент.
6x - 6 = 6, если x = 2.
Уравнение касательной: y = -6x + 1.
Задавайте вопросы в комментариях. :)
Угловой коэффициент касательной - это f'(x0). Это все, что нужно знать, чтобы решить.
1) y = x² + 4
Чтобы найти значение производной в точке касания, найдем саму производную и подставим в нее абсциссу этой точки.
f'(x) = 2x
f'(x0) = 2 - угловой коэффициент.
Угловой коэффициент равен k: 2x = 4, x = 2.
Уравнение касательной к графику в точке с абсциссой x0: y = 2(x - 1) + 5, y = 2x + 3.
2) f'(x) = 4x + 1
f'(x0) = 9 - угловой коэффициент.
f'(x0) = - 1, если 4x + 1 = -1, x = -0.5.
Уравнение касательной: y = 9x - 18 + 10, y = 9x - 8.
3) f'(x) = 6x - 6
f(x0) = -6 - угловой коэффициент.
6x - 6 = 6, если x = 2.
Уравнение касательной: y = -6x + 1.
Задавайте вопросы в комментариях. :)
Спасибо большое)
можем разобрать любой пример из фотографии, если не получается что-то
Похожие вопросы
Предмет: География,
автор: gtasher1gtasher1
Предмет: История,
автор: zhmyax
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Еживичка10