Предмет: Алгебра,
автор: Аноним
1)Вычислить площадь фигуры,ограниченной линиями:
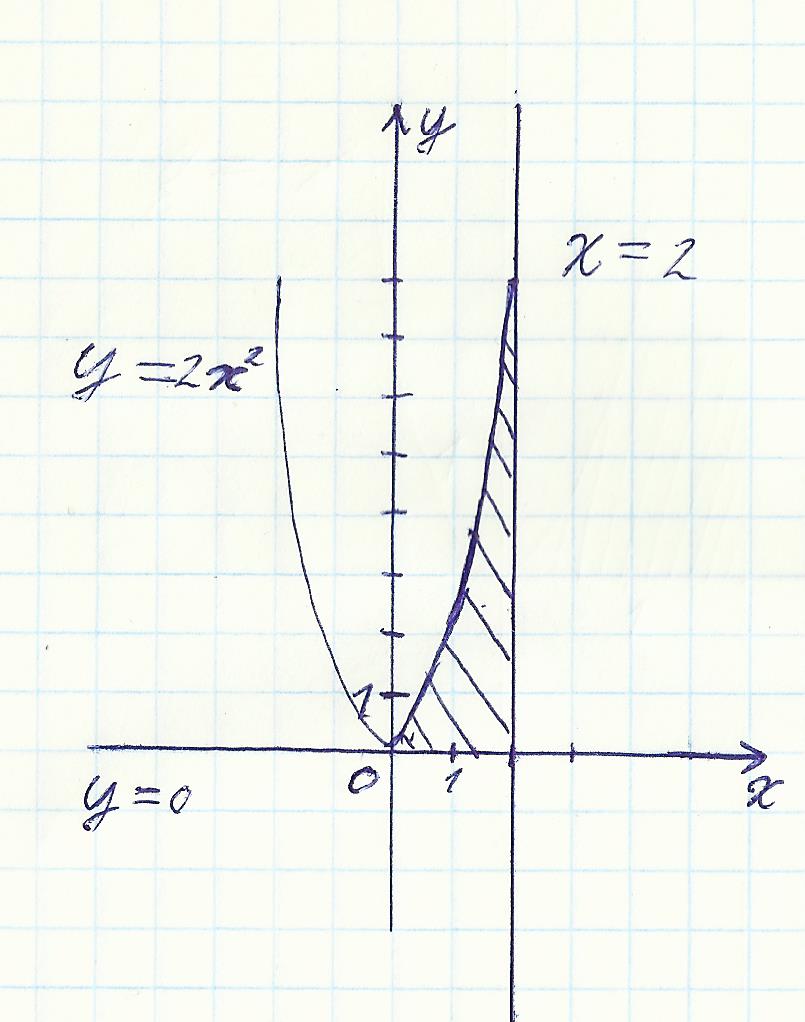
а)y=2x^2,y=0,x=2
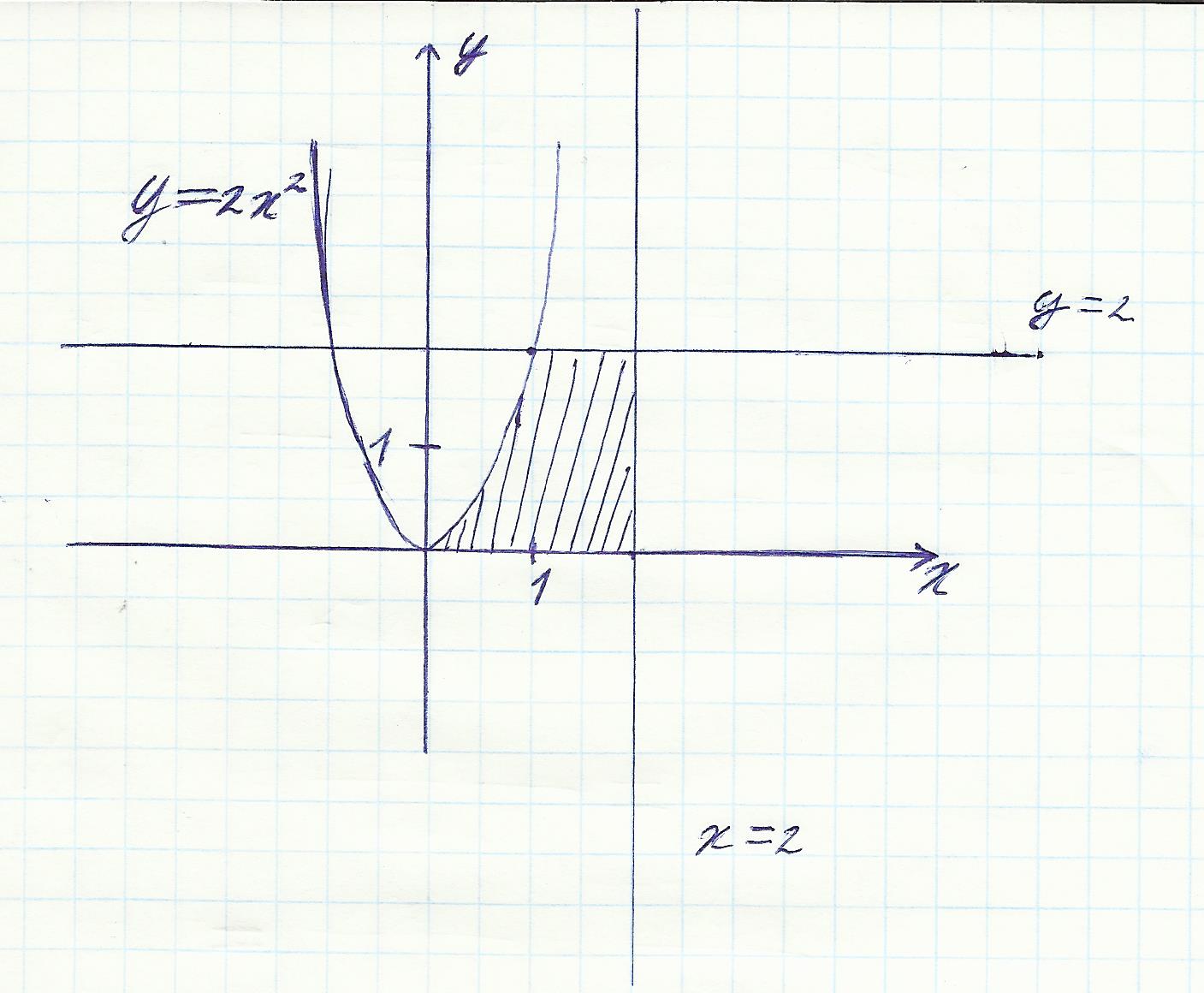
б)y=2x^2,y=2,x=2
2)вычислите площадь фигуры ограниченной линиями
y=sinx,y=-2sinx, 0<=x<=2пи/3
Ответы
Автор ответа:
0
1)
a)

б)
y = 2
y = 2x²
2x²=2
x²=1
x=1

2)

a)
б)
y = 2
y = 2x²
2x²=2
x²=1
x=1
2)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: igilik97
Предмет: Русский язык,
автор: ITZmorivakaSan
Предмет: Литература,
автор: malysharik46
Предмет: Математика,
автор: Flora8485