Предмет: Математика,
автор: mszsp2001
с полным решением
Профильная математика
Приложения:
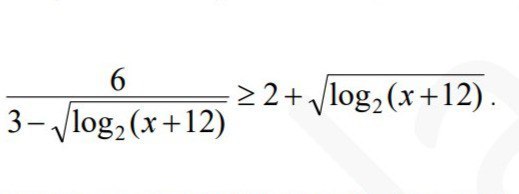
Ответы
Автор ответа:
1
Так же
Откуда
Похожие вопросы