Question

Помогите решить задачу.
Дано:
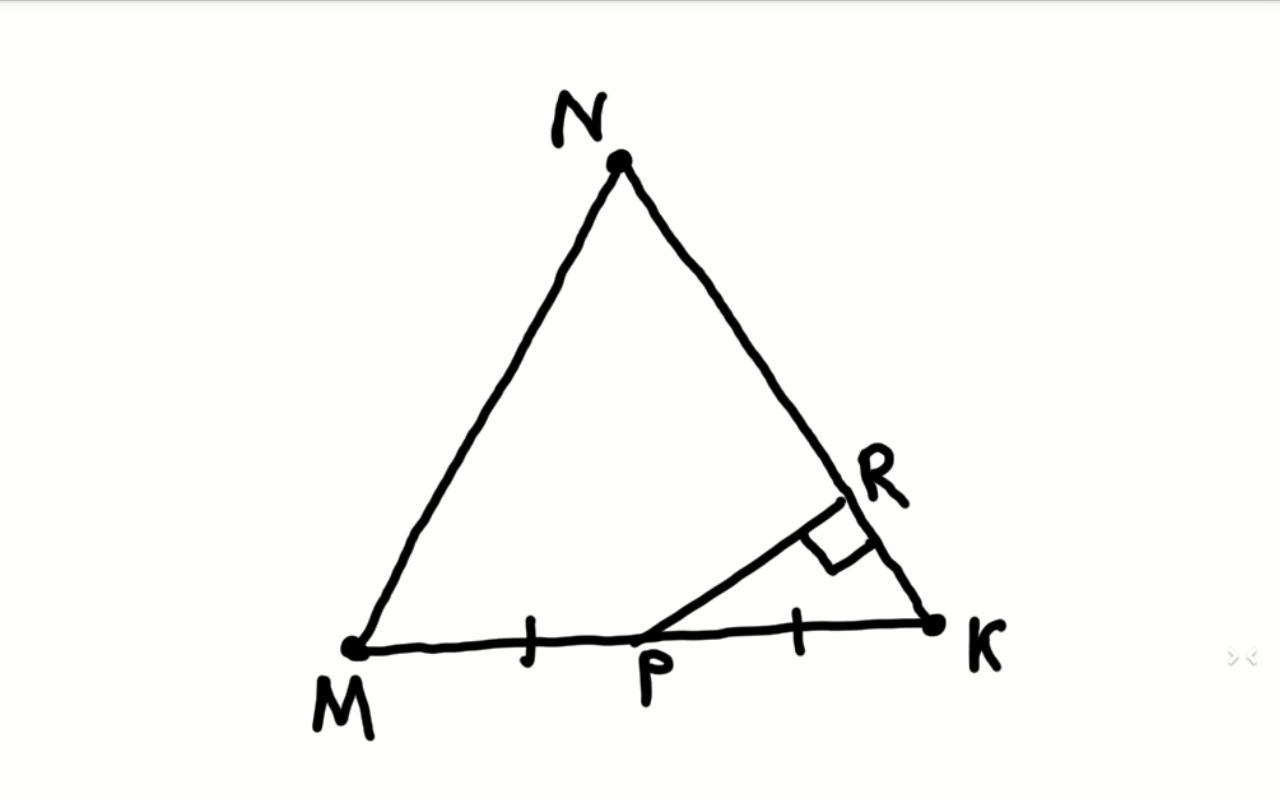
MNK-равносторонний
P-середина MK
PR перпенд. NK
MN=13см
Найти:
NR=?

Answer 1

Т.к MNK- равносторонний, все углы равны по 60°. Т.к в PRK один угол равен 90°, а второй 60°(по теореме о равностороннем треугольнике) ,то третий угол равен 90-60=30°. По теореме о стороне, лежащей против угла в 30° сторона RK равна половине гипотенузы. Гипотенуза PK- по условию равна половине стороны МK, которая равна 13см (из условия и раностороннего треугольника). Значит гипотенуза равна 13÷2=6,5. Значит катет RK=6,5÷2=3,25. Сторона NK также равна 13см т.е сторона NR=NK-RK=13-3,25=9,75

Answer 2

Так как треугольник MNK - равносторонний, то каждый его угол равен 60 градусов. Значит: 
угол $K = 60$ градусов.
угол $PRK = 90$ градусов.
угол $RPK = 180-60-90 = 30$ градусов.
$PK=MK:2 =13:2=6,5$
$RK=PK*cosK=6,5*0,5=3,25$
$NR=13-3,25=9,75$
Ответ: NR=9,75

P.S. Вдруг пригодится для проверки с другим ответом, который написан не используя теорем подобия треугольников и без косинусов =)