Предмет: Алгебра,
автор: помогите4635
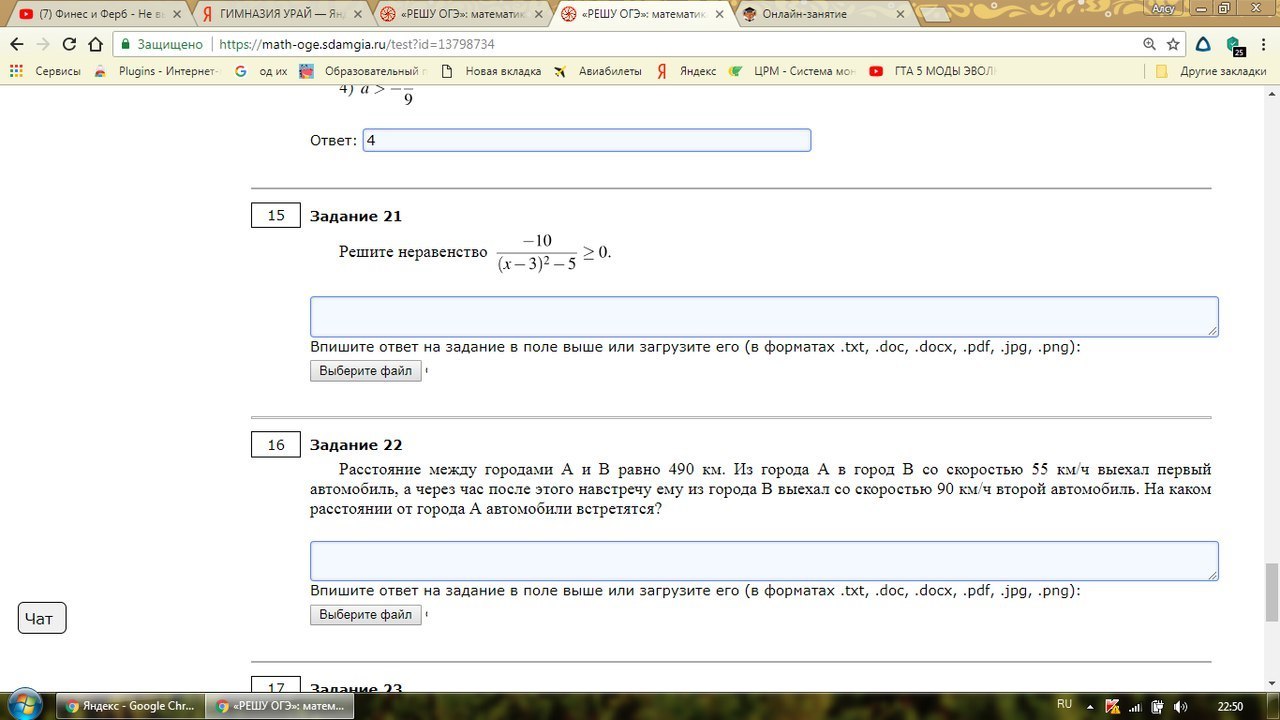
Помогите! Срочно!!! Оба задания
Приложения:
Ответы
Автор ответа:
1
15. 


x^2 - 6x +4 ≠ 0 (на ноль делить нельзя)
Приравняем к нулю и найдем корни:
x^2 - 6x +4 = 0
D = b² - 4ac = 36 - 16 = 20

![x_{12} = \frac{6 ± \sqrt{20} }{2} = \frac{6 ± \sqrt[2]{5}}{2} = \frac{2(3± \sqrt{5}) }{2} = 3± \sqrt{5} x_{12} = \frac{6 ± \sqrt{20} }{2} = \frac{6 ± \sqrt[2]{5}}{2} = \frac{2(3± \sqrt{5}) }{2} = 3± \sqrt{5}](https://tex.z-dn.net/?f=+x_%7B12%7D+%3D++%5Cfrac%7B6+%C2%B1++%5Csqrt%7B20%7D+%7D%7B2%7D+%3D+%5Cfrac%7B6+%C2%B1+%5Csqrt%5B2%5D%7B5%7D%7D%7B2%7D+%3D++%5Cfrac%7B2%283%C2%B1+%5Csqrt%7B5%7D%29+%7D%7B2%7D+%3D++3%C2%B1+%5Csqrt%7B5%7D+)

Значит, x ≠ 3 + √5; 3 - √5.
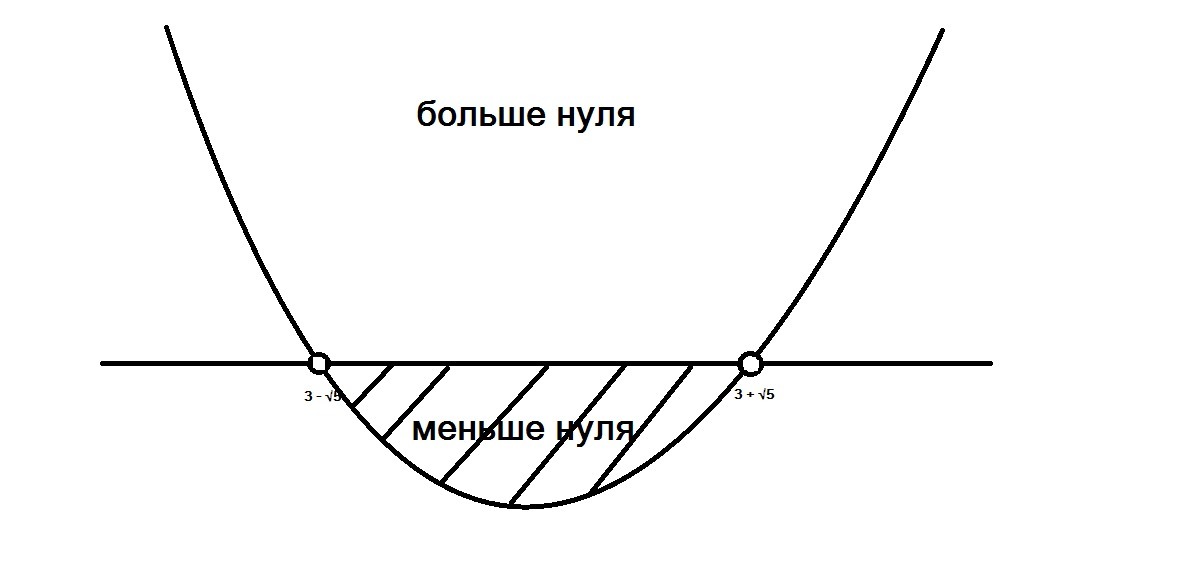
Строим параболу. Видим, что неравенство должно быть больше или равно нулю, в числителе находится отрицательное число, значит, знаменатель тоже должен быть отрицательным, чтобы выражение стало положительным, то есть больше нуля.
x^2 - 6x +4 ≤ 0
Из параболы получаем верный ответ (3 - √5; 3 + √5)
Ответ: (3 - √5; 3 + √5).
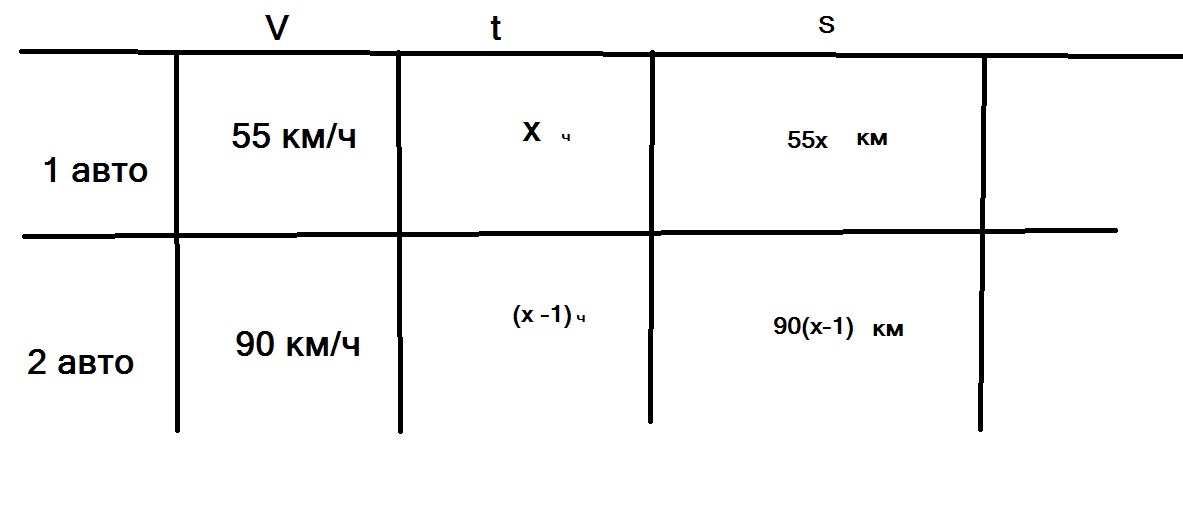
16. Таблица на 2 картинке.
Составим уравнение:
55x + 90(x-1) = 490
55x + 90x - 90 = 490
145x = 580
x = 580/145 = 4
Первый автомобиль встретился со вторым после 4 часов езды. То есть он от города А проехал 4*55 = 220 км. Встретились они на расстоянии 220 км.
Ответ: 220 км.
x^2 - 6x +4 ≠ 0 (на ноль делить нельзя)
Приравняем к нулю и найдем корни:
x^2 - 6x +4 = 0
D = b² - 4ac = 36 - 16 = 20
Значит, x ≠ 3 + √5; 3 - √5.
Строим параболу. Видим, что неравенство должно быть больше или равно нулю, в числителе находится отрицательное число, значит, знаменатель тоже должен быть отрицательным, чтобы выражение стало положительным, то есть больше нуля.
x^2 - 6x +4 ≤ 0
Из параболы получаем верный ответ (3 - √5; 3 + √5)
Ответ: (3 - √5; 3 + √5).
16. Таблица на 2 картинке.
Составим уравнение:
55x + 90(x-1) = 490
55x + 90x - 90 = 490
145x = 580
x = 580/145 = 4
Первый автомобиль встретился со вторым после 4 часов езды. То есть он от города А проехал 4*55 = 220 км. Встретились они на расстоянии 220 км.
Ответ: 220 км.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: samojlenkoaleksandr4
Предмет: Английский язык,
автор: nazymmurat09
Предмет: Биология,
автор: parichehrasuleymanov
Предмет: Математика,
автор: nailyad83
Предмет: Математика,
автор: blance2003