Предмет: Алгебра,
автор: Anna23331
помогите пожалуйста
Приложения:
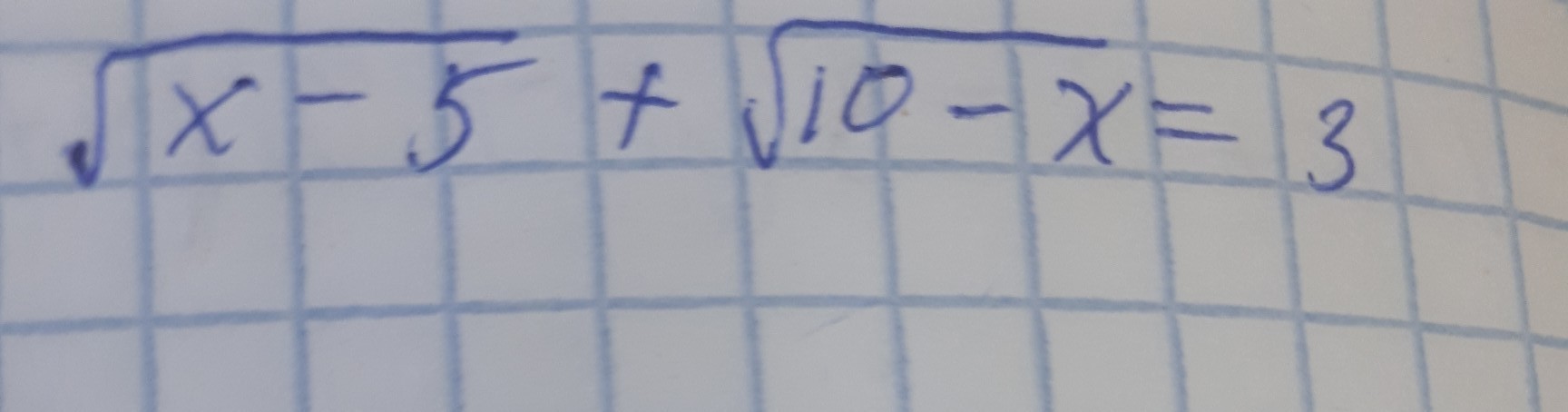
Ответы
Автор ответа:
3
Здесь в равенстве и слева и справа положительные значения, так что можно просто возвести в квадрат левую и правую части, это не нарушит равенство (ведь квадрат положительного числа - положительное число). Итак, имеем:
(√(x-5)+√(10-x))²=3²
Левую часть распишем по формуле квадрата суммы: (a+b)²=a²+2ab+b². Получим:
(√(x-5))²+2√(x-5)·√(10-x)+(√(10-x))²=9
Квадратный корень и квадрат взаимно уничтожаются, получим:
x-5+2√(x-5)√(10-x)+10-x=9
Упрощаем: x и -x сокращаются, -5 и +10 складываем. Получим:
2√(x-5)√(10-x)+5=9
Перенесем +5 в правую часть равенства, получим:
2√(x-5)√(10-x)=4
Сократим обе части равенства на 2, получим:
√(x-5)√(10-x)=2
Представим справа 2 как √4, тогда получим равенство, где справа и слева подкоренные выражения. Но корни выражений равны, если равны и подкоренные выражения, т.е.
√(x-5)√(10-x)=√4
(x-5)(10-x)=4
Раскроем скобки слева, перенесем 4 в левую часть и получим квадратное уравнение:
10x-x²-50+5x=4
-x²+15x-50=4
-x²+15x-50-4=0
-x²+15x-54=0
Для удобства умножим обе части равенства на -1 и получим:
x²-15x+54=0
Решаем квадратное уравнение (через дискриминант или по т.Виета):
D=15²-4·1·54=225-216=9
x₁=(15-√9)/2=(15-3)/2=12/2=6
x₂=(15+√9)/2=(15+3)/2=9
Проверка первого корня (подставим его значение вместо x в начальное выражение):
√(6-5)+√(10-6)=3
√1+√4=3
1+2=3 - верно
Проверка второго корня (подставим его значение вместо x в начальное выражение):
√(9-5)+√(10-9)=3
√4+√1=3
2+1=3 - верно
Ответ: x₁=6 и x₂=9
(√(x-5)+√(10-x))²=3²
Левую часть распишем по формуле квадрата суммы: (a+b)²=a²+2ab+b². Получим:
(√(x-5))²+2√(x-5)·√(10-x)+(√(10-x))²=9
Квадратный корень и квадрат взаимно уничтожаются, получим:
x-5+2√(x-5)√(10-x)+10-x=9
Упрощаем: x и -x сокращаются, -5 и +10 складываем. Получим:
2√(x-5)√(10-x)+5=9
Перенесем +5 в правую часть равенства, получим:
2√(x-5)√(10-x)=4
Сократим обе части равенства на 2, получим:
√(x-5)√(10-x)=2
Представим справа 2 как √4, тогда получим равенство, где справа и слева подкоренные выражения. Но корни выражений равны, если равны и подкоренные выражения, т.е.
√(x-5)√(10-x)=√4
(x-5)(10-x)=4
Раскроем скобки слева, перенесем 4 в левую часть и получим квадратное уравнение:
10x-x²-50+5x=4
-x²+15x-50=4
-x²+15x-50-4=0
-x²+15x-54=0
Для удобства умножим обе части равенства на -1 и получим:
x²-15x+54=0
Решаем квадратное уравнение (через дискриминант или по т.Виета):
D=15²-4·1·54=225-216=9
x₁=(15-√9)/2=(15-3)/2=12/2=6
x₂=(15+√9)/2=(15+3)/2=9
Проверка первого корня (подставим его значение вместо x в начальное выражение):
√(6-5)+√(10-6)=3
√1+√4=3
1+2=3 - верно
Проверка второго корня (подставим его значение вместо x в начальное выражение):
√(9-5)+√(10-9)=3
√4+√1=3
2+1=3 - верно
Ответ: x₁=6 и x₂=9
Похожие вопросы
Предмет: Физика,
автор: bukyc9ipad
Предмет: Математика,
автор: Takhmino4kA
Предмет: Математика,
автор: smrnowa27
Предмет: Математика,
автор: LEB1234