Question

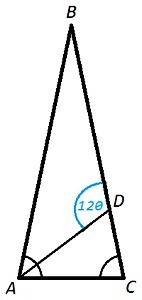
В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD Найдите углы этого треугольника если угол ADB равен 120 градусам

Answer 1

рассмотрим ▲ADC. <ADC равен 60° как смежный <BDA. <DAC=½<BAC по условию задачи. Пусть <DAC=х, тогда  <DCA=2х. Найдем <DCA по теореме о сумме углов треугольника, решим уравнение с одним неизвестным
<DAC+<ADC+<DCA=180°
х+60°+2х=180°
3х=120°
х=40° (<DAC), <DCA=80°
Т.е. углы при основании тр-ка АВС равны по 80°
Значит <ABC=180°-<BAC-<BCA=180°-80°-80°=20°
Ответ: 80°, 80°, 20°

Answer 2

∠A=∠C (углы при основании равнобедренного треугольника)
∠CAD=∠A/2 (AD - биссектриса)
Угол ADB является внешним углом в треугольнике ADC. Внешний угол равен сумме двух внутренних, не смежных с ним.
∠C+∠CAD=∠ADB <=> ∠A+∠A/2=120° <=> ∠A=120°·2/3 =80°
∠A=∠C=80°
∠B=180°-80°*2=20°