Предмет: Алгебра,
автор: IraqIsraelovich
Решите уравнение . Через дискриминант , если это возможно
Приложения:
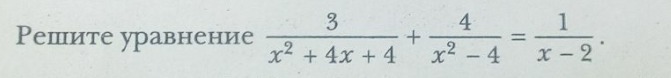
Ответы
Автор ответа:
0
При решении используем формулы сокращенного умножения:
1) квадрат суммы
(а + b)² = a² + 2ab +b²
2) разность квадратов
а² - b² = (a - b)(a + b)

Знаменатели дробей не должны быть равны 0 ( на 0 делить нельзя), следовательно:
х ≠ - 2 ; х ≠ 2
Избавимся от знаменателей, умножим обе части уравнения
на (x-2)(х+2)² :
3(х - 2) + 4(х+2) - 1(х + 2)² = 0 *(х-2)(х+2)²
3х - 6 + 4х + 8 - (х² + 4х + 4) = 0
Перед скобкой знак "-" ⇒ меняем знаки выражения в скобках на противоположные :
3х - 6 + 4х + 8 - х² - 4х - 4 = 0
-х² + (3х + 4х - 4х) + (8 - 6 - 4) = 0
- х² + 3х - 2 = 0 | * (-1)
x² - 3x + 2 = 0
D = (-3)² - 4*1*2 = 9 - 8 = 1 = 1²
D>0 - два корня уравнения
x₁ =
х₂ = - не подходит ( т.к. х ≠ 2)
- не подходит ( т.к. х ≠ 2)
Ответ : х = 1 .
1) квадрат суммы
(а + b)² = a² + 2ab +b²
2) разность квадратов
а² - b² = (a - b)(a + b)
Знаменатели дробей не должны быть равны 0 ( на 0 делить нельзя), следовательно:
х ≠ - 2 ; х ≠ 2
Избавимся от знаменателей, умножим обе части уравнения
на (x-2)(х+2)² :
3(х - 2) + 4(х+2) - 1(х + 2)² = 0 *(х-2)(х+2)²
3х - 6 + 4х + 8 - (х² + 4х + 4) = 0
Перед скобкой знак "-" ⇒ меняем знаки выражения в скобках на противоположные :
3х - 6 + 4х + 8 - х² - 4х - 4 = 0
-х² + (3х + 4х - 4х) + (8 - 6 - 4) = 0
- х² + 3х - 2 = 0 | * (-1)
x² - 3x + 2 = 0
D = (-3)² - 4*1*2 = 9 - 8 = 1 = 1²
D>0 - два корня уравнения
x₁ =
х₂ =
Ответ : х = 1 .
Автор ответа:
0
!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
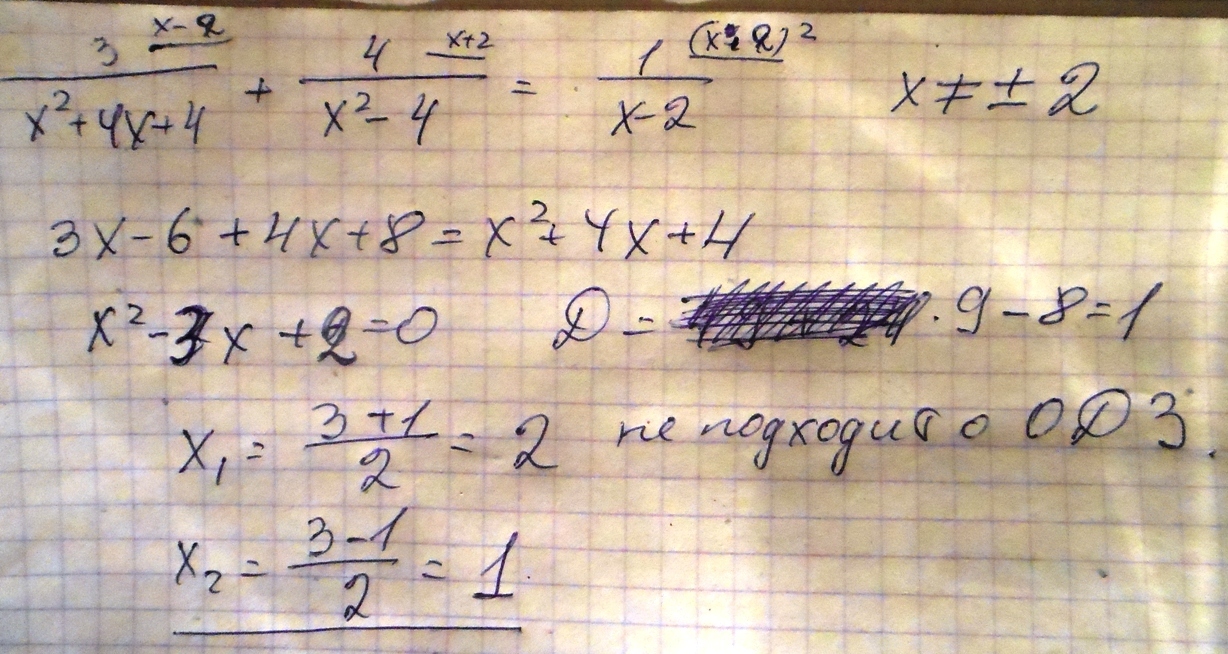
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: ulanapozdeeva43786
Предмет: Геометрия,
автор: lubskaasofia7
Предмет: Алгебра,
автор: nikolai199831
Предмет: Математика,
автор: Maryssy