Предмет: Алгебра,
автор: hhhttt1520
ПЗ. По рисунку 3.30...пожалуйста, надо ответить на все вопросы сразу. Спасибо!!!
Приложения:

Ответы
Автор ответа:
1
ПЗ к рис. 3.30
Вспоминаем КАНОНИЧЕСКОЕ уравнение прямой - Y = k*x + b, где:
k = tgα = ΔY/ΔX - наклон прямой.
В обозначениях координат точки в скобках сначала пишется координата по оси абсцисс - оси Х, а затем, через знак ; - координата по оси ординат - оси У.
Для построения прямой достаточно знать координаты ДВУХ точек. Пусть это точки: А(Ах;Ау) и В(Вх;Ву).
Тогда коэффициенте наклона можно вычислить по формуле:
k = (Ay-By)/(Ax-Bx).
b = Y(0) - сдвиг по оси ординат - оси У - точка пересечения с осью У.
.РЕШЕНИЕ
РИСУНОК с дополнительными обозначениями - в приложении.
1)
Уравнения прямых.
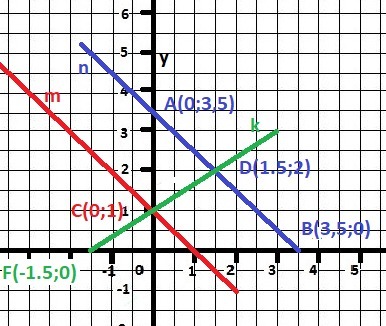
Прямая n проходит через точки А(0;3,5) и В(3,5;0). Вычисляем от А до В, хотя можно и наоборот.
k = (3,5-0)/(0-3,5) = - 1 - коэффициент
b = Ay = 3.5.
Записываем уравнение прямой - n: Y= - x+3.5 - ОТВЕТ
Для прямой -m - без расчетов ("в уме"): Y = -x + 1 - ОТВЕТ
И, наконец, уравнение прямой - k - самое сложное и полезное.
Точка С(0;1) и точка F(-1.5;0)
k = (Cy-Fy)/(Cx-Fx)= (1-0)/(0-(-1.5)) = 1/1.5 = 1/(3/2) = 2/3 - наклон
b =Cy = 0 - сдвиг по оси У.
Уравнение прямой - k : Y = 2/3*x + 1 - ОТВЕТ
2)
После более сложных решений этот пункт делаем без комментариев.
С(-1,5;0) и D(1.5;2) - ОТВЕТ
3)
ВНИМАНИЕ!!! ВАЖНО!!!
При решении систем линейных уравнений используется ПАРАМЕТРИЧЕСКАЯ форма записи уравнения прямой:a*X+b*Y = c.
Запишем наши три уравнения уже в параметрической форме и получим:
Уравнение: y = - x +1 превращается в ....
m) x + y = 1 и аналогично две другие прямые.
n) x + y = 3.5
k) - 1.5*x + y = 1
У прямой - ДВЕ переменных - значит с помощью графиков можно решить систему из ДВУХ уравнений.
Можно составить три системы из двух уравнений:
1) m;n 2) m;k 3) n;k.
ВНИМАНИЕ!!!! ВАЖНО!!!
Две прямых, как и решение системы из двух уравнений может иметь, ужас, ТРИ варианта решения.
1 - они пересекаются в одной и только одной точке - у системы единственное решение.
2 - они параллельны и не имеют точек пересечений - нет решений.
3 - они совпадают - одна прямая - множество решений.
Рассмотрим наши системы уравнений.
1) m;n - прямые параллельны - НЕТ решений.
2) m;k - точка пересечения = С(0;1) или: Х=0, У=1 - ОТВЕТ
3) n;k - точка пересечения = D(1.5;2) или: Х=1,5, У=2 - ОТВЕТ
4)
Можно ли получить систему уравнений с множеством решений - НЕТ - ОТВЕТ
Для этого нужно, чтобы прямые m и n - совпали. Другими словами, чтобы два уравнения имель ПРОПОРЦИОНАЛЬНЫЕ коэффициенты в
параметрической записи прямой.
Другими словами - все ТРИ коэффициента должны быть пропорциональными. В геометрии это как подобные треугольники у которых все три стороны пропорциональны.
.Изменим уравнения
1) х + у = 1
2) 2*х + 2*у = 2
Упрощаем уравнение 2) и оно превращается в уравнение 1)
3) 2*(х+у) = 2*1 - сократили и множество вариантов - это одна прямая.
Вспоминаем КАНОНИЧЕСКОЕ уравнение прямой - Y = k*x + b, где:
k = tgα = ΔY/ΔX - наклон прямой.
В обозначениях координат точки в скобках сначала пишется координата по оси абсцисс - оси Х, а затем, через знак ; - координата по оси ординат - оси У.
Для построения прямой достаточно знать координаты ДВУХ точек. Пусть это точки: А(Ах;Ау) и В(Вх;Ву).
Тогда коэффициенте наклона можно вычислить по формуле:
k = (Ay-By)/(Ax-Bx).
b = Y(0) - сдвиг по оси ординат - оси У - точка пересечения с осью У.
.РЕШЕНИЕ
РИСУНОК с дополнительными обозначениями - в приложении.
1)
Уравнения прямых.
Прямая n проходит через точки А(0;3,5) и В(3,5;0). Вычисляем от А до В, хотя можно и наоборот.
k = (3,5-0)/(0-3,5) = - 1 - коэффициент
b = Ay = 3.5.
Записываем уравнение прямой - n: Y= - x+3.5 - ОТВЕТ
Для прямой -m - без расчетов ("в уме"): Y = -x + 1 - ОТВЕТ
И, наконец, уравнение прямой - k - самое сложное и полезное.
Точка С(0;1) и точка F(-1.5;0)
k = (Cy-Fy)/(Cx-Fx)= (1-0)/(0-(-1.5)) = 1/1.5 = 1/(3/2) = 2/3 - наклон
b =Cy = 0 - сдвиг по оси У.
Уравнение прямой - k : Y = 2/3*x + 1 - ОТВЕТ
2)
После более сложных решений этот пункт делаем без комментариев.
С(-1,5;0) и D(1.5;2) - ОТВЕТ
3)
ВНИМАНИЕ!!! ВАЖНО!!!
При решении систем линейных уравнений используется ПАРАМЕТРИЧЕСКАЯ форма записи уравнения прямой:a*X+b*Y = c.
Запишем наши три уравнения уже в параметрической форме и получим:
Уравнение: y = - x +1 превращается в ....
m) x + y = 1 и аналогично две другие прямые.
n) x + y = 3.5
k) - 1.5*x + y = 1
У прямой - ДВЕ переменных - значит с помощью графиков можно решить систему из ДВУХ уравнений.
Можно составить три системы из двух уравнений:
1) m;n 2) m;k 3) n;k.
ВНИМАНИЕ!!!! ВАЖНО!!!
Две прямых, как и решение системы из двух уравнений может иметь, ужас, ТРИ варианта решения.
1 - они пересекаются в одной и только одной точке - у системы единственное решение.
2 - они параллельны и не имеют точек пересечений - нет решений.
3 - они совпадают - одна прямая - множество решений.
Рассмотрим наши системы уравнений.
1) m;n - прямые параллельны - НЕТ решений.
2) m;k - точка пересечения = С(0;1) или: Х=0, У=1 - ОТВЕТ
3) n;k - точка пересечения = D(1.5;2) или: Х=1,5, У=2 - ОТВЕТ
4)
Можно ли получить систему уравнений с множеством решений - НЕТ - ОТВЕТ
Для этого нужно, чтобы прямые m и n - совпали. Другими словами, чтобы два уравнения имель ПРОПОРЦИОНАЛЬНЫЕ коэффициенты в
параметрической записи прямой.
Другими словами - все ТРИ коэффициента должны быть пропорциональными. В геометрии это как подобные треугольники у которых все три стороны пропорциональны.
.Изменим уравнения
1) х + у = 1
2) 2*х + 2*у = 2
Упрощаем уравнение 2) и оно превращается в уравнение 1)
3) 2*(х+у) = 2*1 - сократили и множество вариантов - это одна прямая.
Приложения:
hhhttt1520:
Для прямой k, кажется вы координаты не те взяли: С(0;1) и D(1,5;2), я не права?
Аааа я поняла, вы просто взяли другую точку, ссори
В 1 пункте для прямой k: b=Cy=0 написали, разве не 1? Ответьте плиз
Похожие вопросы
Предмет: Литература,
автор: Cheburkek
Предмет: Математика,
автор: musafena
Предмет: Литература,
автор: vary22837
Предмет: Математика,
автор: rozhdestvenskay2
Предмет: Математика,
автор: Серега336