Предмет: Геометрия,
автор: lmncsxe
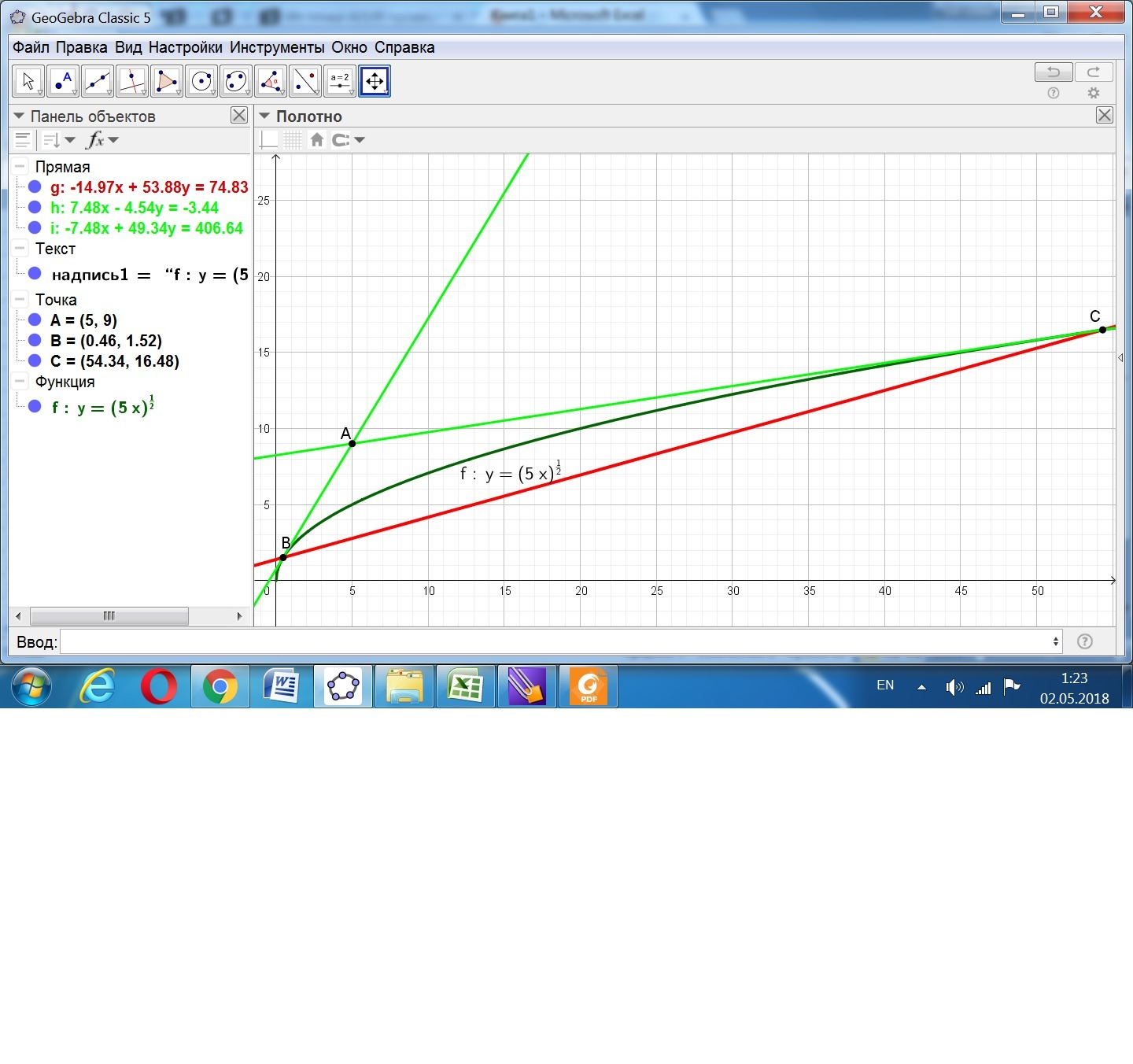
Из точки А(5;9) проведены касательные к параболе y^2=5x. Составить уравнение хорды, соединяющей точки касания.
Ответы
Автор ответа:
1
Даны парабола у² = 5х и точка А(5;9).
Находим уравнения касательных к заданной параболе, проходящих через точку А.
y' = √5/(2√x), y/(xo) = √5/(2√xo).
yкас = (√5/(2√xo))*(x - xo) + (√(5xo)).
Так как касательные проходят через точку А, подставим её координаты вместо переменных х и у:

Решением этого уравнения есть 2 точки касания:
х₁ = (137/5)-(36√14/5) ≈ 0,46006682.
у₁ = √(137 - 36√14) ≈ 1,516685.
х₂ = (137/5)+(36√14/5) ≈ 54,33993.
у₂ = √(137 + 36√14) ≈ 16,48331.
Общее уравнение прямой, проходящей через точки касания, с точностью до двух знаков: -14,97х + 53,88у = 74,83.
Для получения уравнения в каноническом виде (х - хВ)/(хС - хВ) = (у - уВ)/(уС - уВ) надо подставить координаты точек касания.
Находим уравнения касательных к заданной параболе, проходящих через точку А.
y' = √5/(2√x), y/(xo) = √5/(2√xo).
yкас = (√5/(2√xo))*(x - xo) + (√(5xo)).
Так как касательные проходят через точку А, подставим её координаты вместо переменных х и у:
Решением этого уравнения есть 2 точки касания:
х₁ = (137/5)-(36√14/5) ≈ 0,46006682.
у₁ = √(137 - 36√14) ≈ 1,516685.
х₂ = (137/5)+(36√14/5) ≈ 54,33993.
у₂ = √(137 + 36√14) ≈ 16,48331.
Общее уравнение прямой, проходящей через точки касания, с точностью до двух знаков: -14,97х + 53,88у = 74,83.
Для получения уравнения в каноническом виде (х - хВ)/(хС - хВ) = (у - уВ)/(уС - уВ) надо подставить координаты точек касания.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: karinakakdfkd
Предмет: Геометрия,
автор: lizakolbasina9
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: yulyaodintsova1
Предмет: Алгебра,
автор: yhjjjgjj