Предмет: Алгебра,
автор: NadyaNeustr
Помогите решить 5 и 6 номер пожалуйста
Приложения:
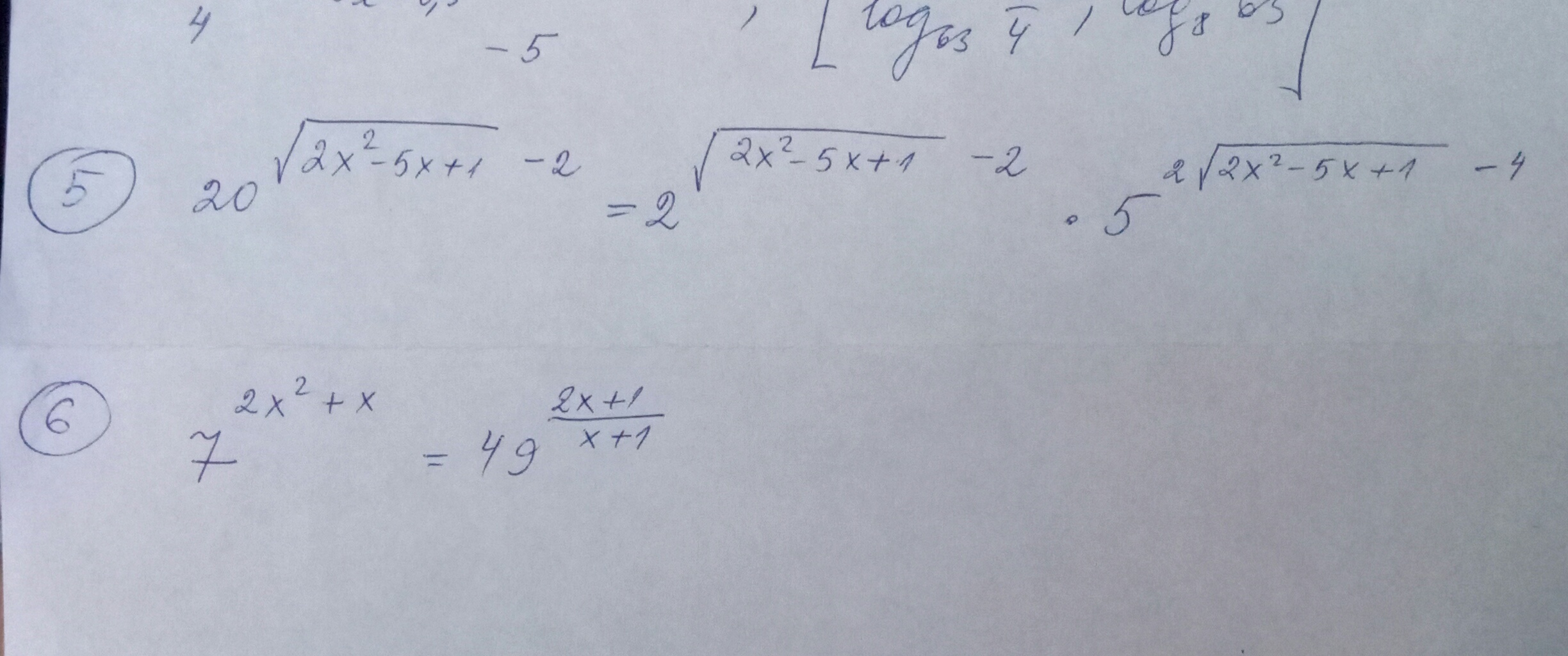
Ответы
Автор ответа:
1
5.
20^(√(2x²-5x+1)-2)=2^(√(2x²-5x+1)-2)*5^(2*√(2x²-5x+1)-4)
ОДЗ: 2x²-5x+1≥0 D=17 x₁=(5-√17)/2≈0,22 x₂=(5+√17)/4≈2,28 ⇒
x∈(-∞;≈0,22]U[≈2.28;+∞)
Пусть √(2x²-5x+1)=n ⇒
20ⁿ⁻²=2ⁿ⁻²*5²*⁽ⁿ⁻²⁾
4ⁿ⁻²*5ⁿ⁻²=2ⁿ⁻²*5²ⁿ⁻⁴
2²ⁿ⁻⁴*5ⁿ⁻²=2ⁿ⁻²*5²ⁿ⁻⁴
2²ⁿ⁻⁴/2ⁿ⁻²=5²ⁿ⁻⁴/5ⁿ⁻²
2²ⁿ⁻⁴⁻ⁿ⁺²=5²ⁿ⁻⁴⁻ⁿ⁺²
2ⁿ⁻²=5ⁿ⁻² ⇒
n-2=0
(√(2x²-5x+1))²=2²
2x²-5x+1=4
2x²-5x-3=0 D=49
x₁=3 ∈ ОДЗ x₂=-0,5 ∈ ОДЗ
Ответ: x₁=3 x₂=-0,5.
6.
7^(2x²+x)=49^((2x+1)/(x+1)) ОДЗ: x+1≠0 x≠-1
7^(x*(2x+1)=7^(2*(2x+1)/(x+1))
x*(2x+1)=2*(2x+1)/(x+1)
x*(2x+1)-2*(2x+1)/(x+1)=0
(2x+1)*(x-2/(x+1))=0
2x+1=0
2x=-1
x₁=-0,5
x-2/(x+1)=0
x=2/(x+1)
x*(x+1)=2
x²+x=2
x²+x-2=0 D=9
x₂=-2 x₃=1
Ответ: x₁=-0,5 x₂=-2 x₃=1.
20^(√(2x²-5x+1)-2)=2^(√(2x²-5x+1)-2)*5^(2*√(2x²-5x+1)-4)
ОДЗ: 2x²-5x+1≥0 D=17 x₁=(5-√17)/2≈0,22 x₂=(5+√17)/4≈2,28 ⇒
x∈(-∞;≈0,22]U[≈2.28;+∞)
Пусть √(2x²-5x+1)=n ⇒
20ⁿ⁻²=2ⁿ⁻²*5²*⁽ⁿ⁻²⁾
4ⁿ⁻²*5ⁿ⁻²=2ⁿ⁻²*5²ⁿ⁻⁴
2²ⁿ⁻⁴*5ⁿ⁻²=2ⁿ⁻²*5²ⁿ⁻⁴
2²ⁿ⁻⁴/2ⁿ⁻²=5²ⁿ⁻⁴/5ⁿ⁻²
2²ⁿ⁻⁴⁻ⁿ⁺²=5²ⁿ⁻⁴⁻ⁿ⁺²
2ⁿ⁻²=5ⁿ⁻² ⇒
n-2=0
(√(2x²-5x+1))²=2²
2x²-5x+1=4
2x²-5x-3=0 D=49
x₁=3 ∈ ОДЗ x₂=-0,5 ∈ ОДЗ
Ответ: x₁=3 x₂=-0,5.
6.
7^(2x²+x)=49^((2x+1)/(x+1)) ОДЗ: x+1≠0 x≠-1
7^(x*(2x+1)=7^(2*(2x+1)/(x+1))
x*(2x+1)=2*(2x+1)/(x+1)
x*(2x+1)-2*(2x+1)/(x+1)=0
(2x+1)*(x-2/(x+1))=0
2x+1=0
2x=-1
x₁=-0,5
x-2/(x+1)=0
x=2/(x+1)
x*(x+1)=2
x²+x=2
x²+x-2=0 D=9
x₂=-2 x₃=1
Ответ: x₁=-0,5 x₂=-2 x₃=1.
Похожие вопросы
Предмет: Физика,
автор: udaniil483
Предмет: Алгебра,
автор: ilyaderevyanko2006
Предмет: История,
автор: denis03082010
Предмет: Математика,
автор: мари177