Question

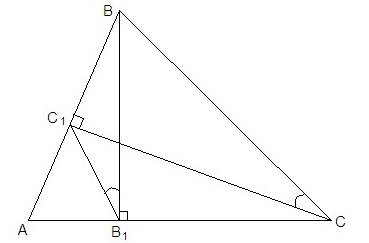
В остроугольном треугольнике авс проведены высоты вв1 и сс1 . Докажите ,что углы вв1с1 им всс1 равны

Answer 1

Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.Треугольники ВВ₁С и ВС₁С - прямоугольные с общей гипотенузой ВС. Поэтому если построить окружность с диаметром ВС, точки В₁ и С₁ будут лежать на этой окружности.Тогда ∠ВВ₁С₁ = ∠ВСС₁ как вписанные, опирающиеся на одну дугу.