Предмет: Математика,
автор: таниана1
помогите пожл решить тема пределы и непрерывность
Приложения:
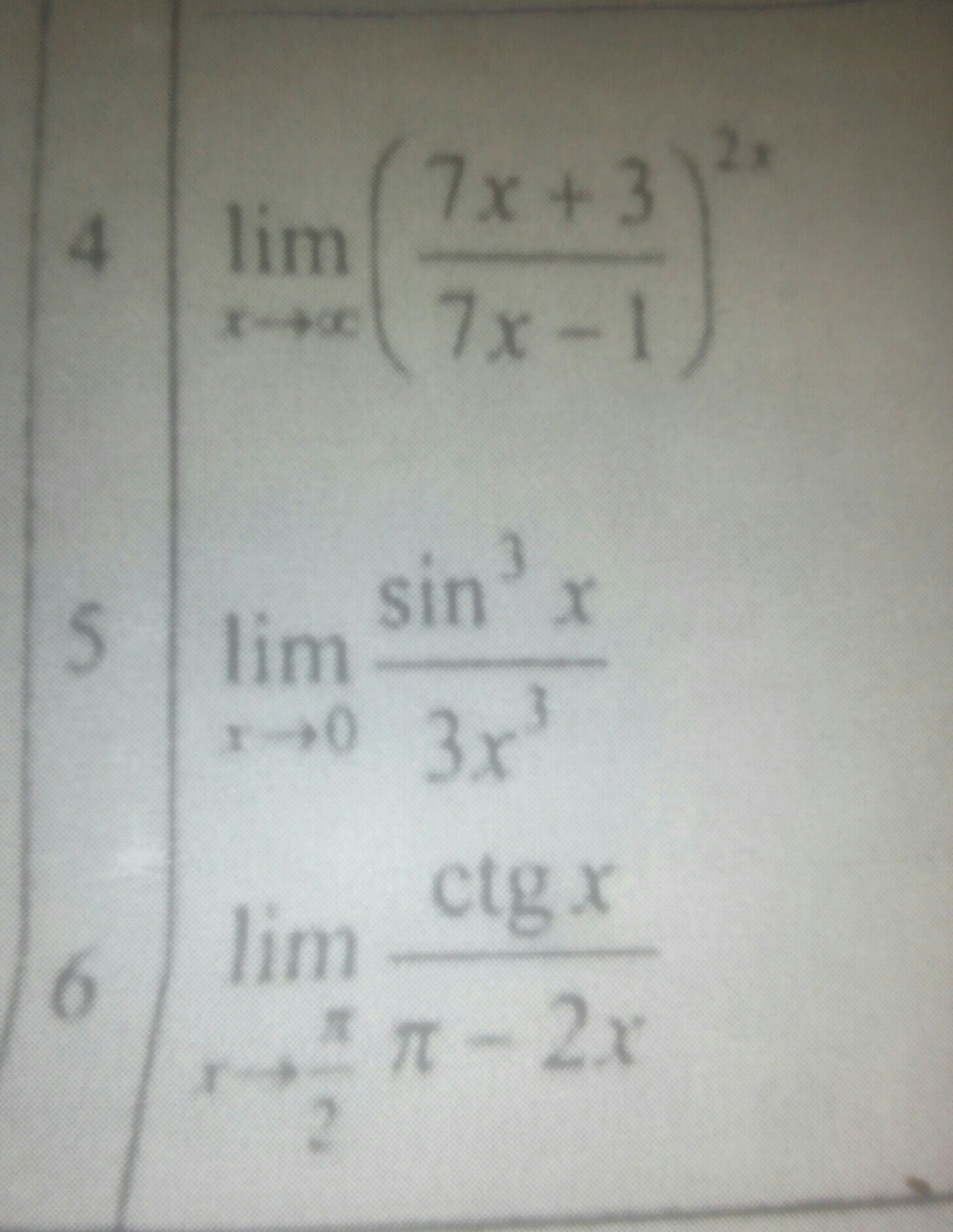
Ответы
Автор ответа:
1
4)

Так как

То

Тогда:

5)

По первому замечательному пределу:

Тогда получаем:

6)

При подстановке значения x в выражение получаем неопределенность .
.
Сделаем замену:

Тогда:

Выполним преобразования:


Так как
То
Тогда:
5)
По первому замечательному пределу:
Тогда получаем:
6)
При подстановке значения x в выражение получаем неопределенность
Сделаем замену:
Тогда:
Выполним преобразования:
Похожие вопросы
Предмет: Алгебра,
автор: fdsfsdfhtrgh
Предмет: География,
автор: ainurbaigazinovaa
Предмет: Русский язык,
автор: serikovaaja4
Предмет: Математика,
автор: WSAD5
Предмет: Математика,
автор: ласточка21