Предмет: Алгебра,
автор: Airborneghost
Найти все значения a, при которых уравнение имеет хотя бы один корень, принадлежащий промежутку (-1; 2]
Приложения:
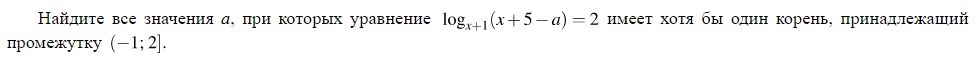
Ответы
Автор ответа:
0
ОДЗ
{x>-1
{x не равно 0
{x>a-5
x+5-a=(x+1)^2
x+5-a=x^2+2x+1
x^2+x-4+a=0
D=1-4(a-4)=17-4a
x1=(-1+√(17-4a))/2
x2=(-1-√(17-4a))/2
a не равна 4
4<a<=17/4
a<4
следует из ОДЗ
-1<(-1-√(17-4a))/2<=2
-1<(-1+√(17-4a))/2<=2
откуда
4<a<=17/4
-2<=a<=17/4
учитывая ОДЗ получаем что при a E [-2,4) U (4,17/4] решения будут лежат на интервале (-1,2].
{x>-1
{x не равно 0
{x>a-5
x+5-a=(x+1)^2
x+5-a=x^2+2x+1
x^2+x-4+a=0
D=1-4(a-4)=17-4a
x1=(-1+√(17-4a))/2
x2=(-1-√(17-4a))/2
a не равна 4
4<a<=17/4
a<4
следует из ОДЗ
-1<(-1-√(17-4a))/2<=2
-1<(-1+√(17-4a))/2<=2
откуда
4<a<=17/4
-2<=a<=17/4
учитывая ОДЗ получаем что при a E [-2,4) U (4,17/4] решения будут лежат на интервале (-1,2].
Похожие вопросы
Предмет: Биология,
автор: danilsevost8
Предмет: Биология,
автор: kriskov409
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: дмитрий253
Предмет: Математика,
автор: Аноним