Предмет: Геометрия,
автор: magicolk
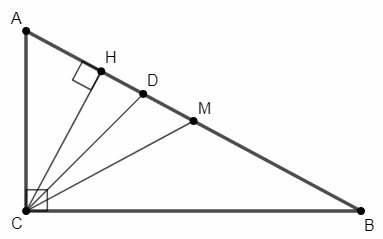
В прямоугольном треугольнике ABC (угол C=90°) проведены медиана CM, биссектриса CD и высота CH. Найдите углы MCD и HCD, если угол ABC=28°.
Ответы
Автор ответа:
17
∠ACD=∠BCD=∠C/2 =90°/2=45° (CD - биссектриса)
Медиана из прямого угла равна половине гипотенузы.
CM=MB, △CMB - равнобедренный.
∠BCM=∠B
∠MCD=∠BCD-∠BCM =45°-∠B =45°-28°=17°
∠CHA=90° (CH - высота), △ACH - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.
∠ACH=90°-∠A=∠B
∠HCD=∠ACD-∠ACH =45°-∠B =17°
Медиана из прямого угла равна половине гипотенузы.
CM=MB, △CMB - равнобедренный.
∠BCM=∠B
∠MCD=∠BCD-∠BCM =45°-∠B =45°-28°=17°
∠CHA=90° (CH - высота), △ACH - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.
∠ACH=90°-∠A=∠B
∠HCD=∠ACD-∠ACH =45°-∠B =17°
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: der454545
Предмет: Биология,
автор: ahdhshs
Предмет: Алгебра,
автор: fdsfsdfhtrgh
Предмет: Химия,
автор: Натусик111111111
Предмет: Математика,
автор: хорошист173