Предмет: Математика,
автор: Lazinesspronik
Помогите с уравнением!xydx=(1+x^2)dy
Приложения:
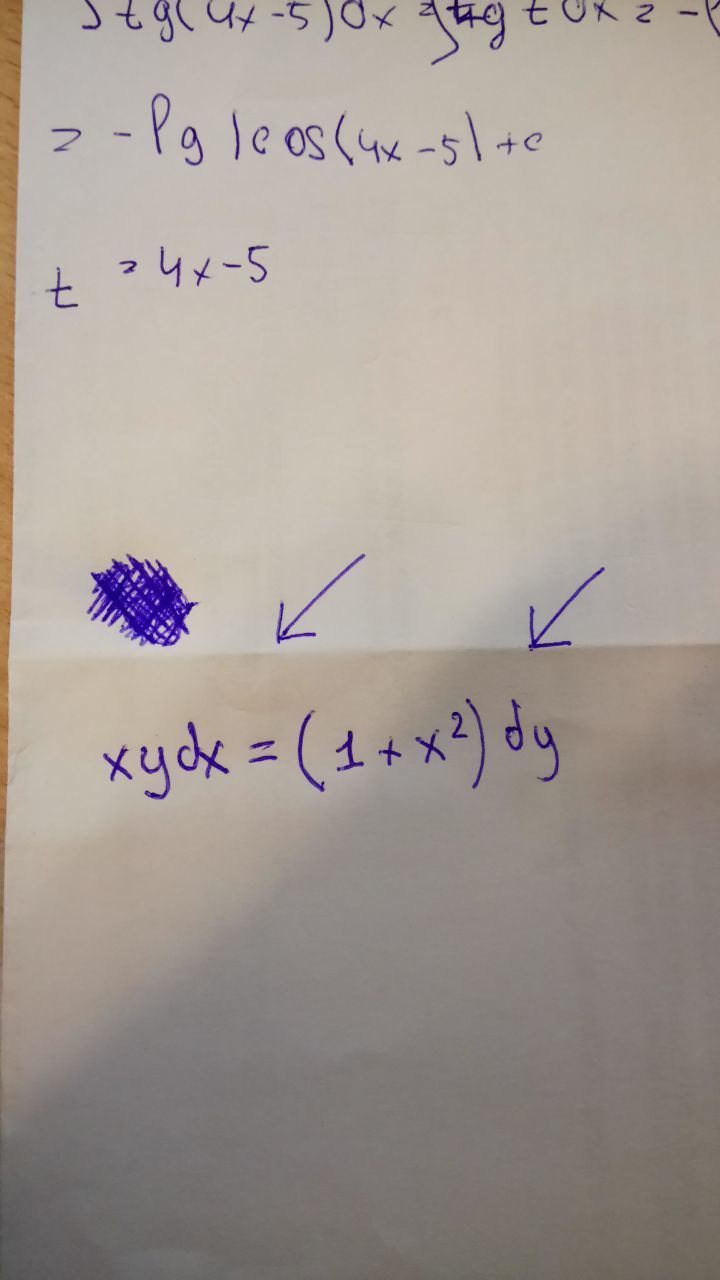
Ответы
Автор ответа:
17
Разделяя переменные, имеем
Lazinesspronik:
при интегрировании xdx/1+x2 не ошибка? d(1+x^2) ? заранее спасибо
Да. 1/2
Поправил
спасибо
Автор ответа:
5
Частное решение у=0 получаемое при делении на у, входит в общее при С*=0
Похожие вопросы
Предмет: Биология,
автор: nnrnekekemens
Предмет: Русский язык,
автор: xurshedxon23
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: leskovskayav