Предмет: Алгебра,
автор: aider12
Помогите пожалуйста ни как не могу решить (б)
Приложения:
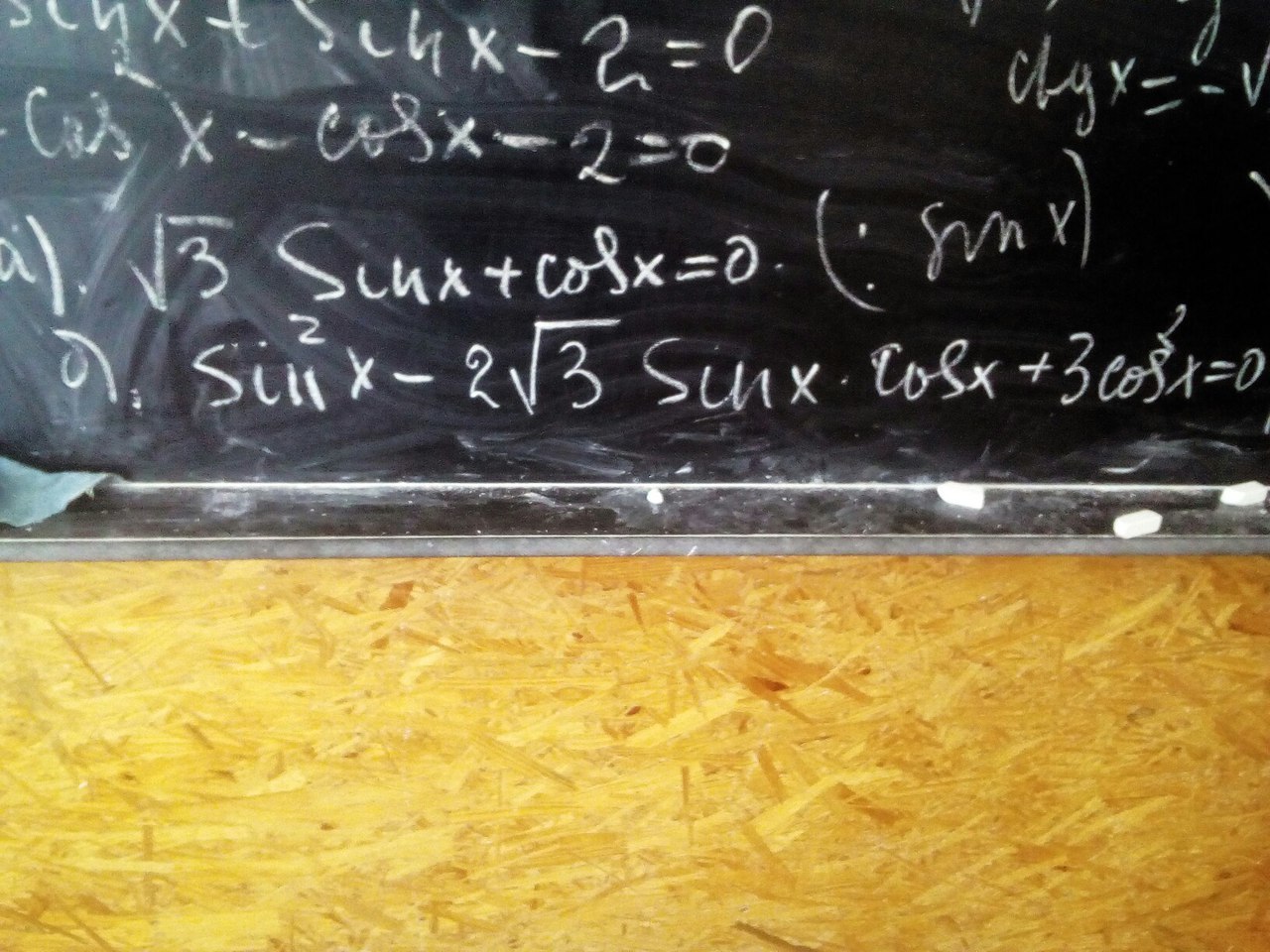
Tanda80:
Если дать подсказку как решать, решите?
я попробую,но не уверен,я знаю что все нужно делить на cos2x,а дальше ступор...
в левой части стоит полный квадрат разности sin(x) и √3*cos(x).
Это под буквой б.
Мда,похоже эта подсказка для меня бесполезна(
Жаль. :(
Ответы
Автор ответа:
0
Решение на. фотографии.
Приложения:
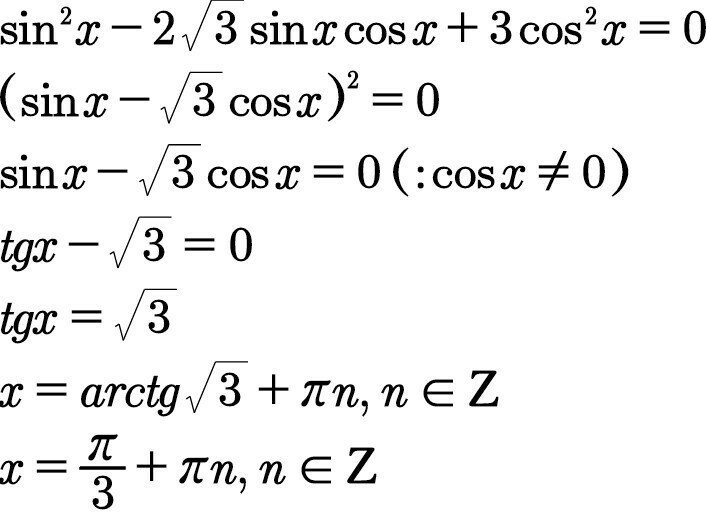
спасибо огромное
Пожалуйста!
Автор ответа:
0
простейшее тригонометрическое уравнение
б.
полный квадрат: a=sinx, b=√3*cosx
или
тригонометрическое квадратное уравнение, замена переменной:
tgx=y
y²-2√3y+3=0
D=(-2√3)²-4*1*3=0
y₁=y₂=√3
обратная замена:
tgx=√3
Похожие вопросы
Предмет: Қазақ тiлi,
автор: lula2659
Предмет: Русский язык,
автор: amantaitalshyb1364
Предмет: Математика,
автор: UCHIHAFLASHER
Предмет: Обществознание,
автор: anastasiya20153