Предмет: Геометрия,
автор: Влад91724
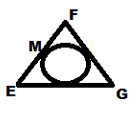
Треугольнике EFG - равнобедренный, с основанием EG. Его периметр равен 44 см, FG=14см. Найдите длину отрезка FМ (М – точка касания вписанной окружности со стороной ВС). (10 баллов)
Приложения:
Ответы
Автор ответа:
2
EF=FG=14 см по условию
EG=P-EF-FG=44-14-14=16 см
Проведём FH ⊥ EG ⇒ ΔEFH - прямоугольный. EH=1/2*EG=8 см .
ΔEOM=ΔEOH по гипотенузе и катету .
Оба прямоугольные:∠ОМЕ=∠ОНЕ=90°(радиус впис. окр. перпендикулярен стороне треугольника), катеты ОМ=ОН=R вписанной окр., ЕО - общая гипотенуза ⇒
ЕМ=ЕН=8 см
FM=EF-EM=14-8=6 cм
EG=P-EF-FG=44-14-14=16 см
Проведём FH ⊥ EG ⇒ ΔEFH - прямоугольный. EH=1/2*EG=8 см .
ΔEOM=ΔEOH по гипотенузе и катету .
Оба прямоугольные:∠ОМЕ=∠ОНЕ=90°(радиус впис. окр. перпендикулярен стороне треугольника), катеты ОМ=ОН=R вписанной окр., ЕО - общая гипотенуза ⇒
ЕМ=ЕН=8 см
FM=EF-EM=14-8=6 cм
Похожие вопросы
Предмет: Обществознание,
автор: disxijs
Предмет: Математика,
автор: babrixa
Предмет: Биология,
автор: jfejdnnwsn
Предмет: Обществознание,
автор: Karinawow99
Предмет: Литература,
автор: papapapapapa2