Предмет: Алгебра,
автор: ася992
Помогите решить логарифмические неравенства
Приложения:
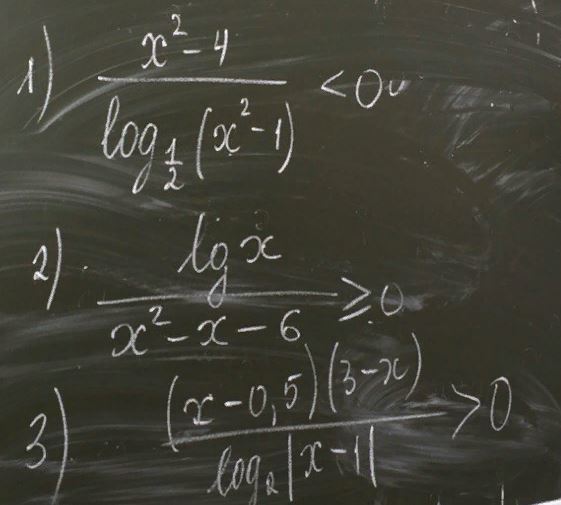
Ответы
Автор ответа:
0
1) (х² -4)/log₀₎₅(x² -1) < 0
метод интервалов. ищем нули числителя и знаменателя, учтём ОДЗ.
х² - 4 = 0, ⇒ х = +-2
log₀₎₅(x² -1) = 0, ⇒ x² -1 = 1,⇒ x² = 2, ⇒ x = +-√2
x² -1 > 0,⇒ (-∞; -1)∪(1; +∞)
- ∞ -2 -√2 -1 1 √2 2 +∞
+ - - - - - + знаки х² -4
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII ОДЗ log₀₎₅(x² -1)
+ + - - - - знаки log₀₎₅(x² -1)
Ответ: (-2; -√2)∪(2;+∞)
2) lgx/(x² -x -6) ≥ 0
метод интервалов.
lgx = 0, ⇒ x = 1
x² -x -6 = 0, ⇒ x = 3 и -2
-∞ ( -2) (0 ) [1 ] ( 3) +∞
- + + знаки lgx
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII ОДЗ lgx
+ - - - + знаки x² -x -6
Ответ: (0; 1]∪ (3; +∞)
3) (х -0,5)(3 -х)/log₂|x -1| > 0
метод интервалов.
(х -0,5)(3 -х) = 0, ⇒ х = 0,5 и 3
log₂|x -1| = 0 , ⇒ |x -1| = 1, ⇒ x = 0 и 2
-∞ [ 0 ] (0,5) (1) [2] (3) +∞
- - + + + - знаки (х -0,5)(3 -х)
+ - - - + + знаки log₂|x -1|
Ответ: [0;0,5)∪[2;3)
метод интервалов. ищем нули числителя и знаменателя, учтём ОДЗ.
х² - 4 = 0, ⇒ х = +-2
log₀₎₅(x² -1) = 0, ⇒ x² -1 = 1,⇒ x² = 2, ⇒ x = +-√2
x² -1 > 0,⇒ (-∞; -1)∪(1; +∞)
- ∞ -2 -√2 -1 1 √2 2 +∞
+ - - - - - + знаки х² -4
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII ОДЗ log₀₎₅(x² -1)
+ + - - - - знаки log₀₎₅(x² -1)
Ответ: (-2; -√2)∪(2;+∞)
2) lgx/(x² -x -6) ≥ 0
метод интервалов.
lgx = 0, ⇒ x = 1
x² -x -6 = 0, ⇒ x = 3 и -2
-∞ ( -2) (0 ) [1 ] ( 3) +∞
- + + знаки lgx
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII ОДЗ lgx
+ - - - + знаки x² -x -6
Ответ: (0; 1]∪ (3; +∞)
3) (х -0,5)(3 -х)/log₂|x -1| > 0
метод интервалов.
(х -0,5)(3 -х) = 0, ⇒ х = 0,5 и 3
log₂|x -1| = 0 , ⇒ |x -1| = 1, ⇒ x = 0 и 2
-∞ [ 0 ] (0,5) (1) [2] (3) +∞
- - + + + - знаки (х -0,5)(3 -х)
+ - - - + + знаки log₂|x -1|
Ответ: [0;0,5)∪[2;3)
Похожие вопросы
Предмет: Физика,
автор: vertu345
Предмет: Физика,
автор: ilonalegkova
Предмет: Физика,
автор: vertu345
Предмет: Математика,
автор: веркп