Предмет: Математика,
автор: Gerinkv
Найти частное решение (частный интеграл) дифференциального уравнения:
y'-xy=2x^3
Приложения:
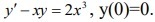
Ответы
Автор ответа:
0
ИСПОЛЬЗОВАН МЕТОД ЛАГРАНЖА.
Найдем сначала общее решение соответствующего однородного уравнения
 - дифференциальное уравнение с разделяющимися переменными.
- дифференциальное уравнение с разделяющимися переменными.

 - общее решение однородного уравнения
- общее решение однородного уравнения
Примем , тогда
, тогда  . По правилу дифференцирования произведения:
. По правилу дифференцирования произведения: 
Подставим данные в исходное уравнение:

Получили дифференциальное уравнение с разделяющимися переменными

Общее решение:
Найдем частное решение, подставляя начальные условия :

 -ЧАСТНОЕ РЕШЕНИЕ.
-ЧАСТНОЕ РЕШЕНИЕ.
Найдем сначала общее решение соответствующего однородного уравнения
Примем
Подставим данные в исходное уравнение:
Получили дифференциальное уравнение с разделяющимися переменными
Общее решение:
Найдем частное решение, подставляя начальные условия :
Похожие вопросы
Предмет: Русский язык,
автор: vitira1985
Предмет: Математика,
автор: madinaxaldarova5
Предмет: Алгебра,
автор: olesya2008zzz
Предмет: Математика,
автор: Петя123410
Предмет: Математика,
автор: 89273195615