Question

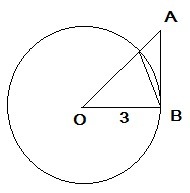
Прямая AB касается окружности с центром O в точке B. Найдите AO, если радиус окружности – 3 см, а хорда, один конец которой совпадает с точкой касания, а второй – с точкой пересечения окружности и прямой AO, стягивает дугу 30°.

Answer 1

∠О-центральный, равен дуге, а которую опирается⇒∠О=30°,⇒
∠A=90-30=60°
По теореме синусов:
ОВ/sinA=OA/sinB⇒
OA=OB*sin90°/sin60°=3*2/√3=2√3