Предмет: Алгебра,
автор: Аноним
Нарисуйте график функции ....................
Приложения:

Ильзат04:
Там 2 примера к кому именно?
Ответы
Автор ответа:
0
Преобразуем функцию


Раскладываем трёхчлены на множители

Имеем функцию:

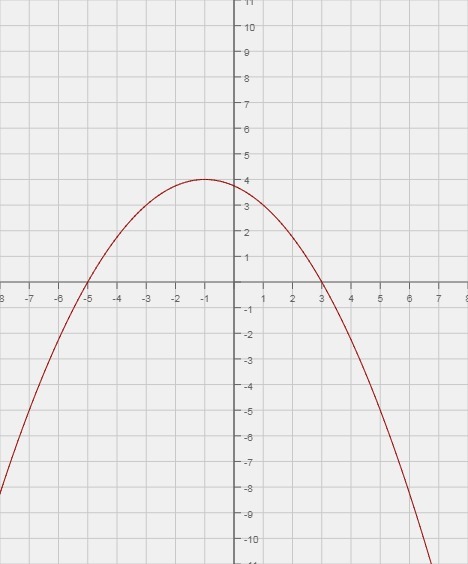
Её графиков является парабола, т.к. a < 0, то ветви параболы смотрят вниз. Определяем вершины параболы, а затем строим график. Но перед этим, надо учесть, что квадратный трёхчлен делится на четыре. Тогда:

Теперь находим вершину параболы

А теперь относительно вершины параболы строим параболу, ветви которой смотрят вниз
Раскладываем трёхчлены на множители
Имеем функцию:
Её графиков является парабола, т.к. a < 0, то ветви параболы смотрят вниз. Определяем вершины параболы, а затем строим график. Но перед этим, надо учесть, что квадратный трёхчлен делится на четыре. Тогда:
Теперь находим вершину параболы
А теперь относительно вершины параболы строим параболу, ветви которой смотрят вниз
Приложения:
Похожие вопросы
Предмет: Математика,
автор: absalimovaadiya
Предмет: Обществознание,
автор: vikaandrusko91
Предмет: Литература,
автор: 919191919191
Предмет: Математика,
автор: angelina252