Предмет: Геометрия,
автор: mrhellplayp7t2po
Решение и ответ срочно
Приложения:
Ответы
Автор ответа:
4
В первой задаче мне кажется не хватает данных, могу только вторую
Приложения:

KnowledgePower:
Вторую и я могу.Сейчас над первой думаю.
Смотри - треугольник SRM- прямоугольный, там все ясно - второй угол - 60, ну и все на этом, у нас больше нет данных QRM - не прямоугольный, как дальше решать?
Я через синус пробовал.
Все 3 стороны нашел,прямоугольного треугольника.А в том пока не знаю.
Автор ответа:
2
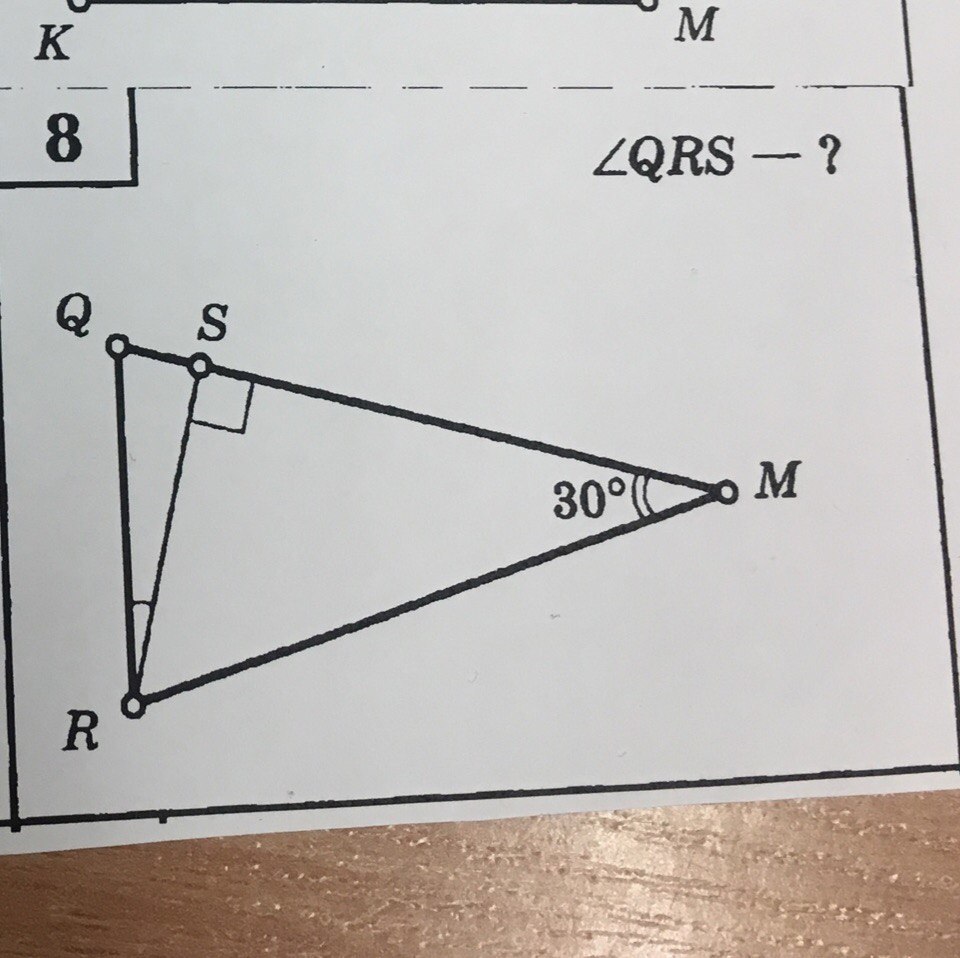
8. Это задача с неполным условием, поэтому однозначного решения не имеет. Из прямоугольного треугольника QSR можно найти угол QRS при условии, что задан угол Q:
∠QRS = 90° - ∠Q
Дальнейшее решение зависит от величины угла Q
1) Если ΔQRM - равнобедренный (на рисунке с условием такой пометки нет), то
∠Q = ∠QRM = (180° - 30°)/2 = 150°/2 = 75°
∠QRS = 90° - ∠Q = 90° - 75° = 15°
2) Но угол Q может иметь любую величину, например, ∠Q = 80°. Тогда
∠QRS = 90° - ∠Q = 90° - 80° = 10°
3) Например, ∠Q = 70°. Тогда
∠QRS = 90° - ∠Q = 90° - 70° = 20°
-------------------------------------------------------------------------------
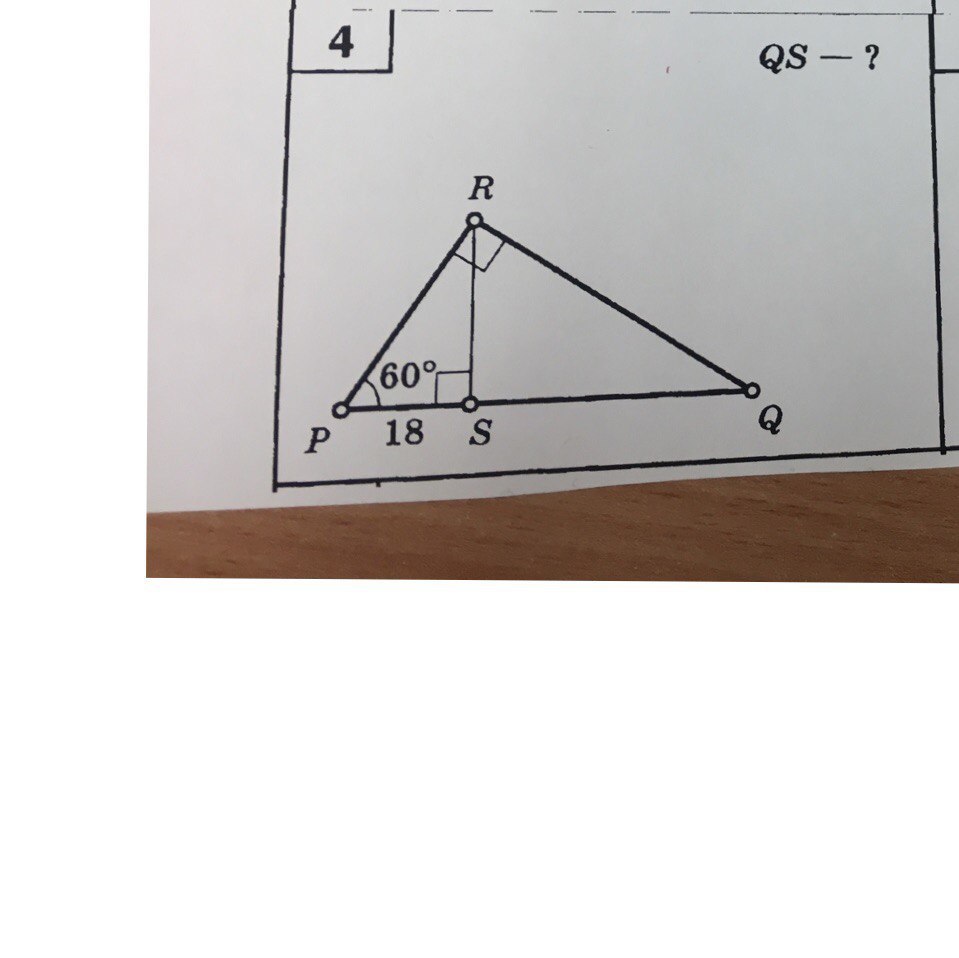
4. ΔPRS - прямоугольный, ∠PSR = 90°; ∠P = 60° ⇒
∠PRS = 90° - 60° = 30°
Катет PS, лежащий против угла 30°, равен половине гипотенузы PR ⇒
PR = 2 * PS = 2 * 18 = 36
ΔPRQ - прямоугольный, ∠PRQ = 90°; ∠P = 60° ⇒
∠Q = 90° - 60° = 30°
Катет PR, лежащий против угла 30°, равен половине гипотенузы PQ ⇒
PQ = 2 * PR = 2 * 36 = 72
QS = PQ - PS = 72 - 18 = 54
QS = 54
∠QRS = 90° - ∠Q
Дальнейшее решение зависит от величины угла Q
1) Если ΔQRM - равнобедренный (на рисунке с условием такой пометки нет), то
∠Q = ∠QRM = (180° - 30°)/2 = 150°/2 = 75°
∠QRS = 90° - ∠Q = 90° - 75° = 15°
2) Но угол Q может иметь любую величину, например, ∠Q = 80°. Тогда
∠QRS = 90° - ∠Q = 90° - 80° = 10°
3) Например, ∠Q = 70°. Тогда
∠QRS = 90° - ∠Q = 90° - 70° = 20°
-------------------------------------------------------------------------------
4. ΔPRS - прямоугольный, ∠PSR = 90°; ∠P = 60° ⇒
∠PRS = 90° - 60° = 30°
Катет PS, лежащий против угла 30°, равен половине гипотенузы PR ⇒
PR = 2 * PS = 2 * 18 = 36
ΔPRQ - прямоугольный, ∠PRQ = 90°; ∠P = 60° ⇒
∠Q = 90° - 60° = 30°
Катет PR, лежащий против угла 30°, равен половине гипотенузы PQ ⇒
PQ = 2 * PR = 2 * 36 = 72
QS = PQ - PS = 72 - 18 = 54
QS = 54
Приложения:
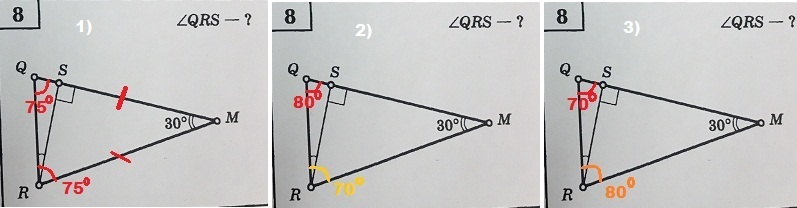
Я нашел там полное условие,там треугольник QRM равнобедренный.Ну и выходит,что боковые углы по 75,а угол QRS = 15 градусов.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Lanaloud
Предмет: История,
автор: sobolevasvetick777
Предмет: Математика,
автор: alinawef23
Предмет: Математика,
автор: Аноним